コンデンサーの静電エネルギー
充電したコンデンサーはエネルギーを持っている
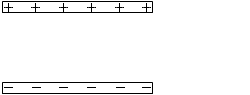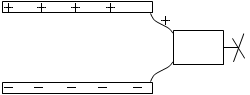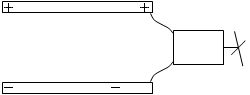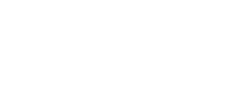 充電したコンデンサーにモーターをつなげるとモーターに付いた羽根は回転します。極板の電荷がモーターに移動し羽根が回転するのです。このことから、充電したコンデンサーはエネルギーを持っているといえます。このエネルギーを静電エネルギーといいます。コンデンサーが何か仕事をした場合、それを放電といいます。
充電したコンデンサーにモーターをつなげるとモーターに付いた羽根は回転します。極板の電荷がモーターに移動し羽根が回転するのです。このことから、充電したコンデンサーはエネルギーを持っているといえます。このエネルギーを静電エネルギーといいます。コンデンサーが何か仕事をした場合、それを放電といいます。
 これは、質量 m の物体を地表から高さ h まで持ち上げて(充電)、mgh のエネルギーを得た物体を、落とすこと(放電)に相当します。
これは、質量 m の物体を地表から高さ h まで持ち上げて(充電)、mgh のエネルギーを得た物体を、落とすこと(放電)に相当します。
 あるいは、ばね定数 k のばねを x だけ伸ばして(充電)、\(\large{\frac{1}{2}}\)kx2 のエネルギーを得たばねを、解放すること(放電)に相当します。
あるいは、ばね定数 k のばねを x だけ伸ばして(充電)、\(\large{\frac{1}{2}}\)kx2 のエネルギーを得たばねを、解放すること(放電)に相当します。
充電したコンデンサーも、極板間は引きつけ合っています。コンデンサーは支えが無いと極板間がくっついてしまいます。
コンデンサーに蓄えられるエネルギー
電気容量 C [F] のコンデンサーに、Q [C] の電荷を溜めたときのエネルギーを求めてみます。
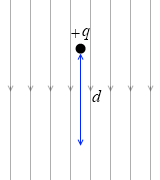 『一様な電場での位置エネルギー』において、U = qEd = qV と説明しましたので、今回求めようとしているエネルギーも U = QV である、と思うかもしれませんが、ちょっと違います。
『一様な電場での位置エネルギー』において、U = qEd = qV と説明しましたので、今回求めようとしているエネルギーも U = QV である、と思うかもしれませんが、ちょっと違います。
U = qV と説明したときは、これは、電場の中において +q [C] の電荷を移動させる仕事、として説明しました。
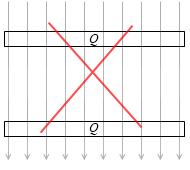 しかし今回は、電場を作っているのが、極板に存在する電荷たち自身です。大きな電場の中にコンデンサーを置いたわけではありません。
しかし今回は、電場を作っているのが、極板に存在する電荷たち自身です。大きな電場の中にコンデンサーを置いたわけではありません。
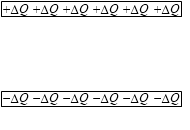 ですのでちょっと考え方を変えまして、電荷 Q を無数の微小電荷 ΔQ に分割して、順を追って考えていきます。
ですのでちょっと考え方を変えまして、電荷 Q を無数の微小電荷 ΔQ に分割して、順を追って考えていきます。
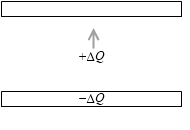 まず、コンデンサーがまったく充電されていないとき、下の極板から上の極板へ ΔQ の電荷を移動させるための仕事の量は 0 です。まだ電場がないので電荷に力が加わりません*重力の影響は無視します。閉じる。下の極板にいる -ΔQ との静電気力がはたらいている、とも考えられますが、どちらにしろ大きさはほぼ 0 です。
まず、コンデンサーがまったく充電されていないとき、下の極板から上の極板へ ΔQ の電荷を移動させるための仕事の量は 0 です。まだ電場がないので電荷に力が加わりません*重力の影響は無視します。閉じる。下の極板にいる -ΔQ との静電気力がはたらいている、とも考えられますが、どちらにしろ大きさはほぼ 0 です。
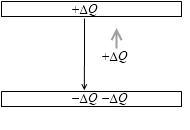 次にまた ΔQ の電荷を移動させるとすると、今度は先に移動した電荷による電場が存在します。Q = CV の関係で導かれる電位差があり、今度は移動に仕事が必要です。でもまだ電位差は小さいので必要な仕事も小さいです。
次にまた ΔQ の電荷を移動させるとすると、今度は先に移動した電荷による電場が存在します。Q = CV の関係で導かれる電位差があり、今度は移動に仕事が必要です。でもまだ電位差は小さいので必要な仕事も小さいです。
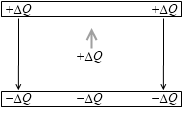 次にまた ΔQ の電荷を移動させるとすると、今度は先に移動した2つの電荷による電場が存在します。先ほどより少し電位差が大きく、移動のための仕事も先ほどより少し余計に掛かります。
次にまた ΔQ の電荷を移動させるとすると、今度は先に移動した2つの電荷による電場が存在します。先ほどより少し電位差が大きく、移動のための仕事も先ほどより少し余計に掛かります。
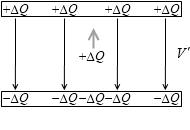 3つ目以降も同様です。1つ前のときよりわずかに仕事が増えます。電位差が V' だとすると仕事は ΔQV' です。
3つ目以降も同様です。1つ前のときよりわずかに仕事が増えます。電位差が V' だとすると仕事は ΔQV' です。
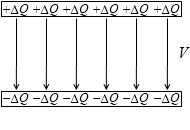 最後の微小電荷 ΔQ を移動させたとき極板には合計 Q の電荷があります。このときの極板間の電位差は \(\large{\frac{Q}{C}}\) です。これを V とします。
最後の微小電荷 ΔQ を移動させたとき極板には合計 Q の電荷があります。このときの極板間の電位差は \(\large{\frac{Q}{C}}\) です。これを V とします。
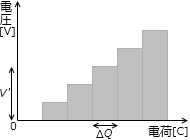 このようにして考えていくと、仕事の総計は左のグラフの柱の面積の合計となります。
このようにして考えていくと、仕事の総計は左のグラフの柱の面積の合計となります。
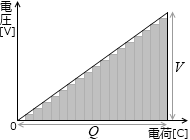 ΔQ の微小さをさらに小さくして考えていくとそれは左のグラフの三角形の部分の面積となります。
ΔQ の微小さをさらに小さくして考えていくとそれは左のグラフの三角形の部分の面積となります。
つまり求めるエネルギーは U = \(\large{\frac{1}{2}}\)QV です。
Q = CV の関係式を代入して別の表現をすれば、 U = \(\large{\frac{1}{2}}\)CV2 = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{Q^2}{C}}\) です。
コンデンサーの極板間引力
極板は引きつけ合っている
上でも述べましたが、コンデンサーの2つの極板は引きつけ合っています。このときの力の大きさを求めてみます。
静電エネルギーの差は仕事の大きさであることから求める
まず、わずかに動かしたときのエネルギー(静電エネルギー)の変化量を求めます。
コンデンサーの静電エネルギーは
U = \(\large{\frac{Q^2}{2C}}\) *
U = \(\large{\frac{1}{2}}\)QV = \(\large{\frac{1}{2}}\)CV2 = \(\large{\frac{Q^2}{2C}}\)
のうち V が含まれていない
U= \(\large{\frac{Q^2}{2C}}\)
をここでは採用します。
まあ、どの式を採用しても結果は同じですが…。
閉じる
であるわけですが、誘電率を ε [F/m]、極板の面積を S [m2]、極板間の距離を d [m] としたときに C = ε\(\large{\frac{S}{d}}\) であるので代入しますと、*
d を含む式にしたいのです。
閉じる
U = \(\large{\frac{Q^2d}{2εS}}\)
これは極板間の距離が d のときの静電エネルギーであり、これよりわずかに極板間の距離が大きい(d + ⊿d)ときの静電エネルギーは
U' = \(\large{\frac{Q^2(d+⊿d)}{2εS}}\)
であり、その差は
U' - U = \(\large{\frac{Q^2(d+⊿d)}{2εS}}\) - \(\large{\frac{Q^2d}{2εS}}\)
= \(\large{\frac{Q^2⊿d}{2εS}}\) *
こんな計算をいちいちするまでもなく
U = \(\large{\frac{Q^2d}{2εS}}\)
なのだから
⊿U = \(\large{\frac{Q^2⊿d}{2εS}}\)
です。
閉じる
です。極板間を d から d + ⊿d に広げるとこれだけエネルギーが増えるということです。
このエネルギーというのは
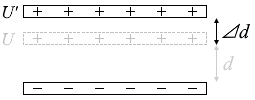 F [N] の力で ⊿d [m] だけゆっくり引っ張ったときの仕事のことであり(エネルギー保存の法則)、
F [N] の力で ⊿d [m] だけゆっくり引っ張ったときの仕事のことであり(エネルギー保存の法則)、
すなわち、
F⋅⊿d = \(\large{\frac{Q^2⊿d}{2εS}}\)
であります。計算すると、
F = \(\large{\frac{Q^2}{2εS}}\) ……①
です。
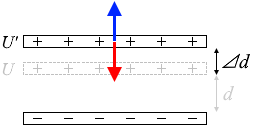 この力はゆっくり引っ張ったときの力であるので、大きさは極板間引力と同じです。向きは逆です。
この力はゆっくり引っ張ったときの力であるので、大きさは極板間引力と同じです。向きは逆です。
ガウスの法則と F = QE から求める
ガウスの法則を用いた別解も紹介しておきます。
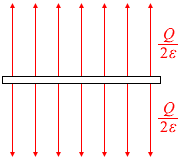 2つの極板のうち片方の極板に着目すると、その極板の両面からは 2πkQ 本ずつ*
k は
2つの極板のうち片方の極板に着目すると、その極板の両面からは 2πkQ 本ずつ*
k は
クーロンの法則
F = k\(\large{\frac{q_1q_2}{r^2}}\)
によって定められる比例定数です。
閉じるの電気力線が湧き出て(あるいは吸い込んで)います。
誘電率 ε = \(\large{\frac{1}{4πk}}\) を使って書き換えると、\(\large{\frac{Q}{2ε}}\) 本です。
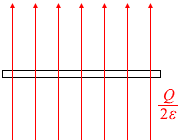 つまりこれは、もう片方の極板に着目すると、この極板は \(\large{\frac{Q}{2ε}}\) 本の電気力線の中に置かれた Q の電荷を持つ物体ということになります。
つまりこれは、もう片方の極板に着目すると、この極板は \(\large{\frac{Q}{2ε}}\) 本の電気力線の中に置かれた Q の電荷を持つ物体ということになります。
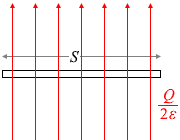 電気力線というものは「電場の強さが E の場所に 1m2 当たり E 本の電気力線を描く」と設定されたものだから、S の面積のところに \(\large{\frac{Q}{2ε}}\) 本の電気力線がある今回の場合、電場の強さ(E1 と置く)は
電気力線というものは「電場の強さが E の場所に 1m2 当たり E 本の電気力線を描く」と設定されたものだから、S の面積のところに \(\large{\frac{Q}{2ε}}\) 本の電気力線がある今回の場合、電場の強さ(E1 と置く)は
E1 = \(\large{\frac{\frac{Q}{2ε}}{S}}\) = \(\large{\frac{Q}{2εS}}\)
ということになります。
そして電場の強さが E1 のところに置かれた Q の電荷が受ける力の大きさは F = QE1 であるから、
F = QE1 = \(\large{\frac{Q^2}{2εS}}\)
となり、上の①式と同じ結果が得られます。
諸注意
E を含めた別の表現
①式を E を含めて表現してみます。εS を取り除いて E を付けます。E は極板間の電場の強さです。
まず Q = CV の式に C = ε\(\large{\frac{S}{d}}\) を代入して、(『電気容量』参照)
Q = ε\(\large{\frac{S}{d}}\)V
これに V = Ed の式を代入すると、
Q = εSE
∴ \(\large{\frac{1}{εS}}\) = \(\large{\frac{E}{Q}}\)
これを①式に代入すると、
F = \(\large{\frac{Q^2}{2εS}}\) = \(\large{\frac{1}{2}}\)QE
となります。
U も F も思っていたのと違って、半分
E の電場の中に置かれた q の電荷が受ける力が F = qE であることから類推して極板間引力は F = QE ではないかと考えてしまうとこれは間違いです。たしかに極板間の電場は E ですが F = QE とはなりません。F = QE という力はたとえば極板と極板の間に Q の電荷を置いたような場合に電荷が受ける力です。けっして極板に掛かる力ではありません。極板に掛かる力はあくまでも F = \(\large{\frac{1}{2}}\)QE です。
上で説明したように、静電エネルギーについて安直に考えると U = QV であるような気がしてしまいます。
極板間引力も安直に考えると F = QE であるような気がしてしまいます。
実際には共にその半分です。
作用反作用の法則に慣れてないと力を2倍にしたくなるが
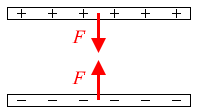 正の極板も、負の極板も互いに F の力で引っ張っているときに、極板間引力の大きさは 2F であると考えてはいけません。力というものは必ず”対”になってはたらきます。F という大きさの力が”対”になってはたらいています。作用⋅反作用の法則です。
正の極板も、負の極板も互いに F の力で引っ張っているときに、極板間引力の大きさは 2F であると考えてはいけません。力というものは必ず”対”になってはたらきます。F という大きさの力が”対”になってはたらいています。作用⋅反作用の法則です。
 充電したコンデンサーにモーターをつなげるとモーターに付いた羽根は回転します。極板の電荷がモーターに移動し羽根が回転するのです。このことから、充電したコンデンサーはエネルギーを持っているといえます。このエネルギーを静電エネルギーといいます。コンデンサーが何か仕事をした場合、それを放電といいます。
充電したコンデンサーにモーターをつなげるとモーターに付いた羽根は回転します。極板の電荷がモーターに移動し羽根が回転するのです。このことから、充電したコンデンサーはエネルギーを持っているといえます。このエネルギーを静電エネルギーといいます。コンデンサーが何か仕事をした場合、それを放電といいます。 これは、質量 m の物体を地表から高さ h まで持ち上げて(充電)、mgh のエネルギーを得た物体を、落とすこと(放電)に相当します。
これは、質量 m の物体を地表から高さ h まで持ち上げて(充電)、mgh のエネルギーを得た物体を、落とすこと(放電)に相当します。 あるいは、ばね定数 k のばねを x だけ伸ばして(充電)、\(\large{\frac{1}{2}}\)kx2 のエネルギーを得たばねを、解放すること(放電)に相当します。
あるいは、ばね定数 k のばねを x だけ伸ばして(充電)、\(\large{\frac{1}{2}}\)kx2 のエネルギーを得たばねを、解放すること(放電)に相当します。 『一様な電場での位置エネルギー』において、U = qEd = qV と説明しましたので、今回求めようとしているエネルギーも U = QV である、と思うかもしれませんが、ちょっと違います。
『一様な電場での位置エネルギー』において、U = qEd = qV と説明しましたので、今回求めようとしているエネルギーも U = QV である、と思うかもしれませんが、ちょっと違います。 しかし今回は、電場を作っているのが、極板に存在する電荷たち自身です。大きな電場の中にコンデンサーを置いたわけではありません。
しかし今回は、電場を作っているのが、極板に存在する電荷たち自身です。大きな電場の中にコンデンサーを置いたわけではありません。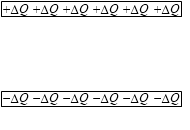 ですのでちょっと考え方を変えまして、電荷 Q を無数の微小電荷 ΔQ に分割して、順を追って考えていきます。
ですのでちょっと考え方を変えまして、電荷 Q を無数の微小電荷 ΔQ に分割して、順を追って考えていきます。 まず、コンデンサーがまったく充電されていないとき、下の極板から上の極板へ ΔQ の電荷を移動させるための仕事の量は 0 です。まだ電場がないので電荷に力が加わりません*重力の影響は無視します。閉じる。下の極板にいる -ΔQ との静電気力がはたらいている、とも考えられますが、どちらにしろ大きさはほぼ 0 です。
まず、コンデンサーがまったく充電されていないとき、下の極板から上の極板へ ΔQ の電荷を移動させるための仕事の量は 0 です。まだ電場がないので電荷に力が加わりません*重力の影響は無視します。閉じる。下の極板にいる -ΔQ との静電気力がはたらいている、とも考えられますが、どちらにしろ大きさはほぼ 0 です。 次にまた ΔQ の電荷を移動させるとすると、今度は先に移動した電荷による電場が存在します。Q = CV の関係で導かれる電位差があり、今度は移動に仕事が必要です。でもまだ電位差は小さいので必要な仕事も小さいです。
次にまた ΔQ の電荷を移動させるとすると、今度は先に移動した電荷による電場が存在します。Q = CV の関係で導かれる電位差があり、今度は移動に仕事が必要です。でもまだ電位差は小さいので必要な仕事も小さいです。 次にまた ΔQ の電荷を移動させるとすると、今度は先に移動した2つの電荷による電場が存在します。先ほどより少し電位差が大きく、移動のための仕事も先ほどより少し余計に掛かります。
次にまた ΔQ の電荷を移動させるとすると、今度は先に移動した2つの電荷による電場が存在します。先ほどより少し電位差が大きく、移動のための仕事も先ほどより少し余計に掛かります。 3つ目以降も同様です。1つ前のときよりわずかに仕事が増えます。電位差が V' だとすると仕事は ΔQV' です。
3つ目以降も同様です。1つ前のときよりわずかに仕事が増えます。電位差が V' だとすると仕事は ΔQV' です。 最後の微小電荷 ΔQ を移動させたとき極板には合計 Q の電荷があります。このときの極板間の電位差は \(\large{\frac{Q}{C}}\) です。これを V とします。
最後の微小電荷 ΔQ を移動させたとき極板には合計 Q の電荷があります。このときの極板間の電位差は \(\large{\frac{Q}{C}}\) です。これを V とします。 このようにして考えていくと、仕事の総計は左のグラフの柱の面積の合計となります。
このようにして考えていくと、仕事の総計は左のグラフの柱の面積の合計となります。 ΔQ の微小さをさらに小さくして考えていくとそれは左のグラフの三角形の部分の面積となります。
ΔQ の微小さをさらに小さくして考えていくとそれは左のグラフの三角形の部分の面積となります。 F [N] の力で ⊿d [m] だけ
F [N] の力で ⊿d [m] だけ この力は
この力は 2つの極板のうち片方の極板に着目すると、その極板の両面からは 2πkQ 本ずつ
2つの極板のうち片方の極板に着目すると、その極板の両面からは 2πkQ 本ずつ つまりこれは、もう片方の極板に着目すると、この極板は \(\large{\frac{Q}{2ε}}\) 本の電気力線の中に置かれた Q の電荷を持つ物体ということになります。
つまりこれは、もう片方の極板に着目すると、この極板は \(\large{\frac{Q}{2ε}}\) 本の電気力線の中に置かれた Q の電荷を持つ物体ということになります。
 正の極板も、負の極板も互いに F の力で引っ張っているときに、極板間引力の大きさは 2F であると考えてはいけません。力というものは必ず”対”になってはたらきます。F という大きさの力が”対”になってはたらいています。
正の極板も、負の極板も互いに F の力で引っ張っているときに、極板間引力の大きさは 2F であると考えてはいけません。力というものは必ず”対”になってはたらきます。F という大きさの力が”対”になってはたらいています。