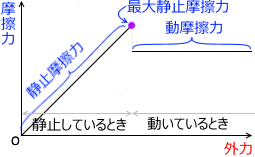
動き出す前後で違う
動き出すと軽くなる
 物体が動き出す前と動き出した後では摩擦力の大きさが違います。動き出すと摩擦力は小さくなるのです。日常生活でも経験があると思いますが、なかなか動かないと思えた物体も、いざ動き始めると少し軽くなったように感じます。
物体が動き出す前と動き出した後では摩擦力の大きさが違います。動き出すと摩擦力は小さくなるのです。日常生活でも経験があると思いますが、なかなか動かないと思えた物体も、いざ動き始めると少し軽くなったように感じます。
静止摩擦力
 動き出す前の摩擦力を静止摩擦力といいます。動かないということはつり合っているということだから(床面と平行な)外力と静止摩擦力は大きさが同じです。常に同じです*
たとえば、
動き出す前の摩擦力を静止摩擦力といいます。動かないということはつり合っているということだから(床面と平行な)外力と静止摩擦力は大きさが同じです。常に同じです*
たとえば、
1.1Nで引っ張ったときの摩擦力が1.1Nで、動かず、
1.2Nで引っ張ったときの摩擦力が1.2Nで、動かず、
1.3Nで引っ張ったときの摩擦力が1.3Nで、動かず、
1.4Nで引っ張ったときの摩擦力が1.4Nで、動かず、
1.5Nで引っ張ったときの摩擦力が1.4999Nで、突如動き出す、
という感じです。
1.3Nで引っ張ったときに、摩擦力が1.3001Nになってしまうようなことは起こり得ません。これだと、引っ張った方向と逆方向に物体が動き出すことになります。心霊現象です。摩擦力は能動的な力ではなく受動的な力です。
下で説明する動摩擦力については、外力と摩擦力が常に同じになるとは限りません。それでも摩擦力が外力より大きくなるようなことはありません。
閉じる。その最大値(一番長くなったとき)は動き出してからの動摩擦力より大きい(長い)です。
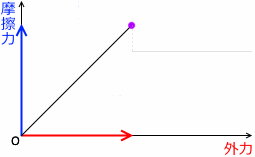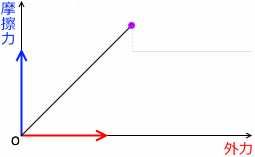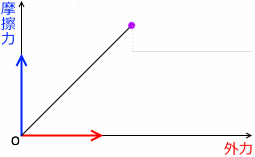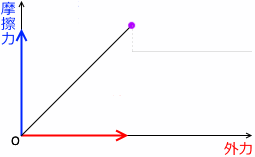 横軸に外力、縦軸に静止摩擦力をとったグラフを描くとその曲線は(y=xの)傾き45°*
横軸と縦軸のスケールが同じ場合に、45°になるということです。言いたいのは、外力=静止摩擦力 ということです。
横軸に外力、縦軸に静止摩擦力をとったグラフを描くとその曲線は(y=xの)傾き45°*
横軸と縦軸のスケールが同じ場合に、45°になるということです。言いたいのは、外力=静止摩擦力 ということです。
そして45°というのは、摩擦係数のことではありません。勘違いしないようにしてください。
・摩擦係数というのは垂直抗力と摩擦力に関する係数です。
・いまの45°というのは外力と摩擦力に関する係数です。
・下で説明する静止摩擦係数というのは垂直抗力と最大静止摩擦力に関する係数です。
閉じるの直線となります。
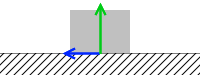
外力を徐々に大きくしていって、やっと動き出したときの静止摩擦力を最大静止摩擦力(あるいは単に最大摩擦力)といいます。左図の紫点の摩擦力のことです。
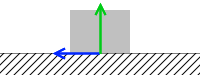 最大静止摩擦力を F0 、垂直抗力を N とすると、以下のように表せます。
最大静止摩擦力を F0 、垂直抗力を N とすると、以下のように表せます。
最大静止摩擦力
F0 = μN
このときの μ を静止摩擦係数といいます。あくまでも静止摩擦力が最大(紫点)のときの係数です。
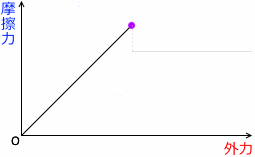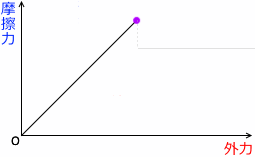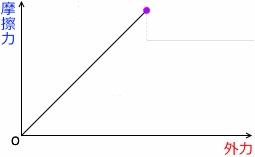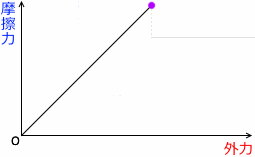 静止摩擦係数が大きくなる(あるいは垂直抗力が大きくなる)ということは、グラフでいうと、曲線が延長される、ということです。決して曲線の傾きが大きくなるということではありません。
静止摩擦係数が大きくなる(あるいは垂直抗力が大きくなる)ということは、グラフでいうと、曲線が延長される、ということです。決して曲線の傾きが大きくなるということではありません。
動摩擦力
 動き出してからの摩擦力を動摩擦力といいます。上で説明した最大静止摩擦力より小さい(短い)です。一定速度で動いているならつり合っているということだから外力と動摩擦力は大きさが同じです。加速するなら外力の方が大きいです。減速するなら動摩擦力の方が大きいです。
動き出してからの摩擦力を動摩擦力といいます。上で説明した最大静止摩擦力より小さい(短い)です。一定速度で動いているならつり合っているということだから外力と動摩擦力は大きさが同じです。加速するなら外力の方が大きいです。減速するなら動摩擦力の方が大きいです。
 物体が動いている最中の動摩擦力の大きさは変化しません。運動のスピードが変化しても、外力の大きさが変化しても動摩擦力は変化しません。これが静止摩擦力との大きな違いです。*実際には変化するのですが、高校物理においては、変化しないものとして取り扱います。
物体が動いている最中の動摩擦力の大きさは変化しません。運動のスピードが変化しても、外力の大きさが変化しても動摩擦力は変化しません。これが静止摩擦力との大きな違いです。*実際には変化するのですが、高校物理においては、変化しないものとして取り扱います。
閉じる
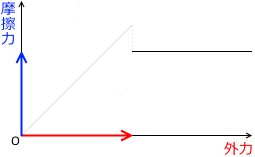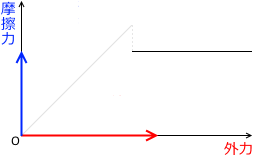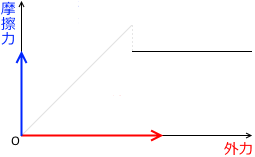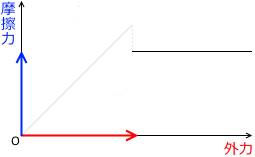 横軸に外力、縦軸に動摩擦力をとったグラフを描くとその曲線は傾き 0 の水平線になります。大きさは最大静止摩擦力より少し小さいです。
横軸に外力、縦軸に動摩擦力をとったグラフを描くとその曲線は傾き 0 の水平線になります。大きさは最大静止摩擦力より少し小さいです。
*
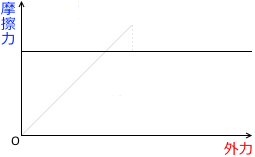 実際には、外力が小さいときにも動摩擦力はありますし、
実際には、外力が小さいときにも動摩擦力はありますし、
 なかなか直線というわけにもいかないですし、
なかなか直線というわけにもいかないですし、
 同じ外力でも、物体の移動速度が 10m/s のときと 30m/s ときでは動摩擦力の大きさは違いますし、
同じ外力でも、物体の移動速度が 10m/s のときと 30m/s ときでは動摩擦力の大きさは違いますし、
最大静止摩擦力より動摩擦力の方が大きい場合もあるだろうし、
摩擦の原理は単純じゃないですし、
一概にグラフの曲線を単純化することはできません。
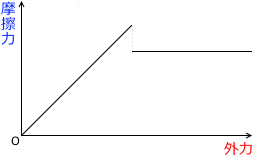 しかし、とりあえず高校物理では左図のようなものであるとして強引に単純化します。
しかし、とりあえず高校物理では左図のようなものであるとして強引に単純化します。
静止摩擦力の部分の曲線が直線であることは確実です。
閉じる
 動摩擦力を F' 、垂直抗力を N とすると、以下のように表せます。
動摩擦力を F' 、垂直抗力を N とすると、以下のように表せます。
動摩擦力
F' = μ'N
このときの μ' を動摩擦係数といいます。たいていの物質において、上で説明した静止摩擦係数 μ よりやや小さい値になっています。
 最大静止摩擦力より動摩擦力の方が小さい理由は、筆者の個人的な予想ですが、動いているときは一瞬宙に浮くので、そのときに加速され勢いがつき、その分引っ掛かりに打ち勝つため、だと思います。
最大静止摩擦力より動摩擦力の方が小さい理由は、筆者の個人的な予想ですが、動いているときは一瞬宙に浮くので、そのときに加速され勢いがつき、その分引っ掛かりに打ち勝つため、だと思います。
グラフのおさらい
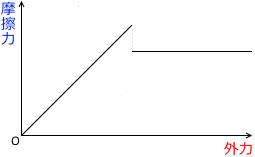 このグラフの読み取り方は以下のようになります。
このグラフの読み取り方は以下のようになります。