力の合成・分解

力の合成

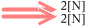2N の力と 2N の力を合わせれば 4N の力になります。これを力の合成といい、合わせた力を合力といいます。

力の合成はベクトルの加法

上記のように同じ作用線上にあって同じ方向を向いている力同士の合成なら話は簡単です。しかし力はベクトルであり、どれもが同じ方向を向いているとは限りません。違う方向を向く力同士の合成はどう考えればよいでしょう。

たとえば 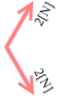このような2つの力があった場合、数学のベクトルの加法にならいます。すなわち平行四辺形の対角線が合力となります。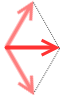

もし 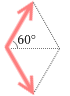2つの力の角度が120°であるなら 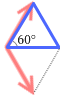この青い三角形は正三角形であり、平行四辺形の対角線の長さは各辺の長さと同じになるので、

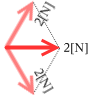合力は 2N となります。2N ＋ 2N が 2N となるのです。4N とはなりません。 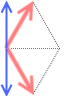縦方向の成分は打ち消し合ってしまい、 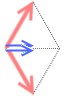横方向の成分だけ残るからです。（ ページ末参照。）

ベクトルの加法を習ってない人のために以下に例を示します。

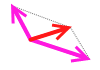
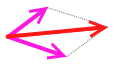
また、平行四辺形で考えなくても1つの辺を平行移動させて三角形を作るという考え方もあります。

ただし力を平行移動させていいのは平行四辺形の代わりに三角形を想像するときだけです。基本的に力は作用線上以外は移動させてはいけません。

力の分解

力の合成の反対が力の分解です。

このような力を 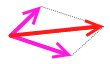このように分解したり 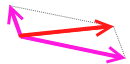このように分解したりします。分解した力を分力といいます。

直交座標

高校物理において力の分解をするときは、斜交座標 ではなく、直交座標 である場合がほとんどです。

ですので、 このような力は このように分解することが多いです。

x軸、y軸を定めて力の分解を行うと、

力 \(\vec{F}\) の x軸上の分力が \(\vec{F_x}\)、y軸上の分力が \(\vec{F_y}\) です。

\(\vec{F}\) と x軸とのなす角を θ としますと、

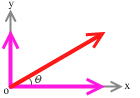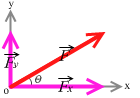
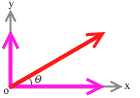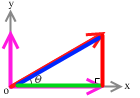F_x = Fcosθ、F_y = Fsinθ と表すことができます。

例

上図において、もし F=10[N] で θ=30° であるならば、

cos30° = \(\large{\frac{\sqrt{3}}{2}}\) ≒ \(\large{\frac{1.73}{2}}\) = 0.87 であるので、分力 \(\vec{F_x}\) の大きさは 10×cos30° ≒ 10×0.87 = 8.7[N]、

sin30° = \(\large\frac{1}{2}\) = 0.5 であるので、分力 \(\vec{F_y}\) の大きさは 10×0.5 = 5.0[N] となります。

（上の力の合成で説明したように 8.7[N]+5.0[N]≠10[N] となっています）

一旦分解してから合成してもいい

\(\vec{A}\) というベクトルが \(\vec{A_x}\) と \(\vec{A_y}\) に分解でき、\(\vec{B}\) というベクトルが \(\vec{B_x}\) と \(\vec{B_y}\) に分解できるとき、\(\vec{A}\) と \(\vec{B}\) を合成するときには分解したもの同士を合成しても同じ結果になります。
　　\(\vec{A}\) + \(\vec{B}\) = \(\vec{A_x}\) + \(\vec{A_y}\) + \(\vec{B_x}\) + \(\vec{B_y}\)
です。分配法則です。