正弦波
単振動
波をよく伝える媒質はばねの性質を持ちます。ばねの性質が無いものは波をよく伝えることができません。ばねは、伸ばされれば伸ばされるほど強い力で引き戻そうとします。この力を復元力といいますが、復元力を持つものは単振動という動きをします。簡単に説明します。
 物体が円周上を一定の速さでまわり続ける運動を等速円運動と呼びますが、この物体に横から光を当てると壁に映った影は周期的な往復運動をします。
物体が円周上を一定の速さでまわり続ける運動を等速円運動と呼びますが、この物体に横から光を当てると壁に映った影は周期的な往復運動をします。
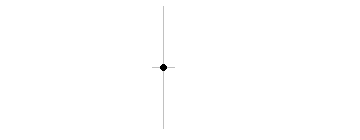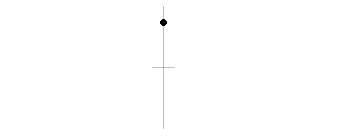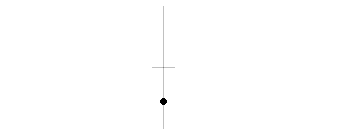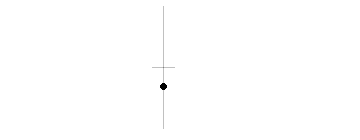 この動きを単振動といいます。物理において等速直線運動の次に基本となる重要な運動です。
この動きを単振動といいます。物理において等速直線運動の次に基本となる重要な運動です。
正弦波
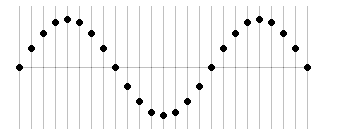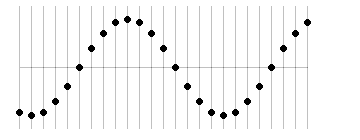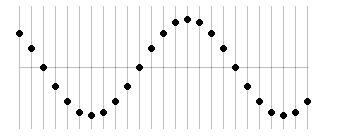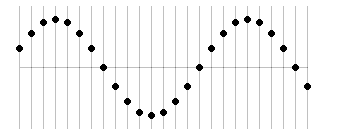 各点が隣の点を引っ張っり上げたり引き下ろしたりしながら次々に伝わるのが波です。波をよく伝える媒質はばねの性質を持ち、各点がこの単振動という動きをしています。目を凝らして1つの縦の線に注目して見てください。
各点が隣の点を引っ張っり上げたり引き下ろしたりしながら次々に伝わるのが波です。波をよく伝える媒質はばねの性質を持ち、各点がこの単振動という動きをしています。目を凝らして1つの縦の線に注目して見てください。
このときできる波の形はきれいに整っていて、正弦波と呼びます。数学で習う正弦曲線(サインカーブ)と同じ形なのでこのように呼びます。
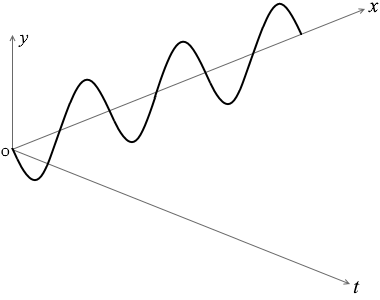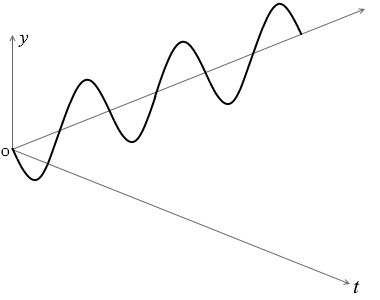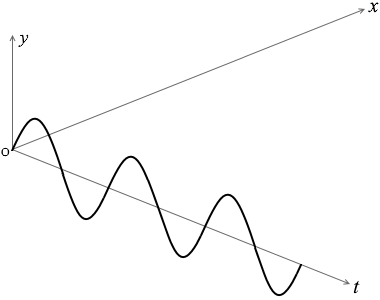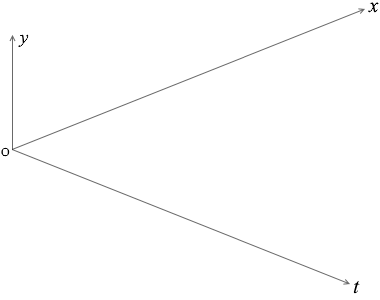
横軸が \(x\) か \(t\) か
波のグラフを見るときは注意しなければならないことがあります。それはグラフの横軸が \(x\) であるのか \(t\) であるのかということです。
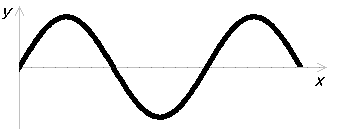 \(x\) である場合は、グラフはある時刻における波の形を表しています。
\(x\) である場合は、グラフはある時刻における波の形を表しています。
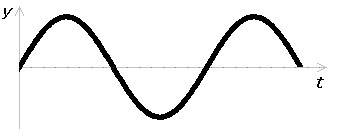 \(t\) である場合は、グラフはある地点における時間による変化を表しています。
\(t\) である場合は、グラフはある地点における時間による変化を表しています。
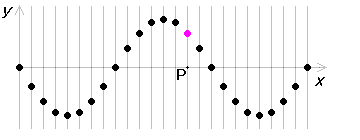 たとえば初め左図のような形の波があったとすれば、これは \(t\)=0 における波の形、ということになります。(後の説明のためにP点を定めてマークします)
たとえば初め左図のような形の波があったとすれば、これは \(t\)=0 における波の形、ということになります。(後の説明のためにP点を定めてマークします)
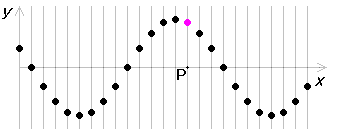 1秒後に左図のようになれば、\(t\)=1 における波の形、ということです。
1秒後に左図のようになれば、\(t\)=1 における波の形、ということです。
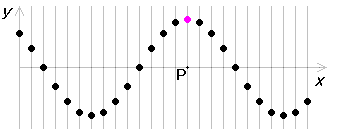 \(t\)=2 における波の形。
\(t\)=2 における波の形。
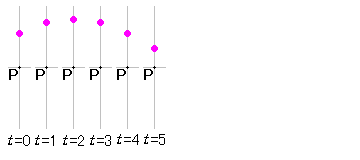 そして P点だけに着目し、\(t\)=0、\(t\)=1、\(t\)=2、\(t\)=3、\(t\)=4、\(t\)=5、のときの高さを描き出すと左図のようになり、
そして P点だけに着目し、\(t\)=0、\(t\)=1、\(t\)=2、\(t\)=3、\(t\)=4、\(t\)=5、のときの高さを描き出すと左図のようになり、
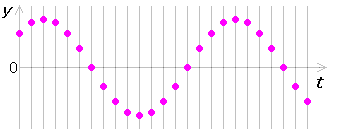 整理してグラフにすると左図のようになります。横軸は \(x\) でなく、\(t\) です。これは P点における時間変化を表すグラフです。上の波の形を表すグラフと同じ形なので紛らわしいです。
整理してグラフにすると左図のようになります。横軸は \(x\) でなく、\(t\) です。これは P点における時間変化を表すグラフです。上の波の形を表すグラフと同じ形なので紛らわしいです。
これらのことを立体的に表わすと下図のようになります。
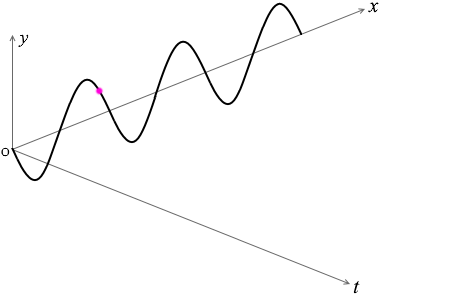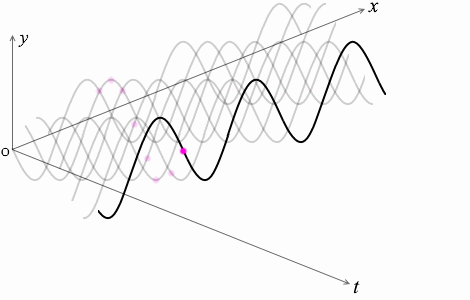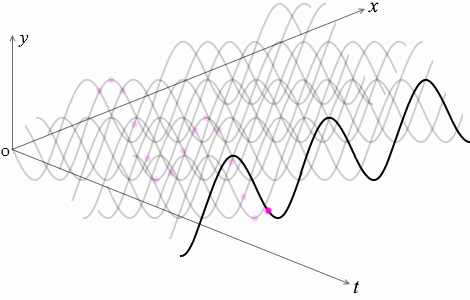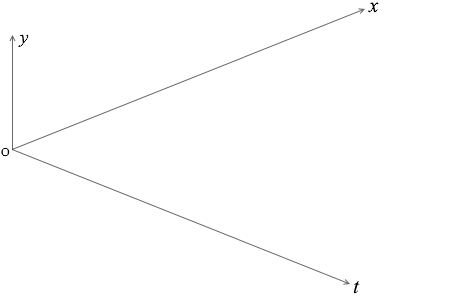
波に関するグラフを読み取るときは、横軸が \(x\) であるか \(t\) であるか、注意が必要です。
正弦波の式
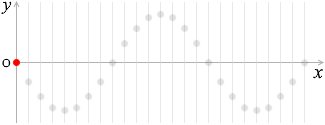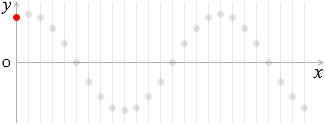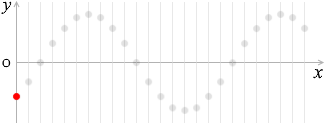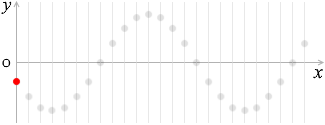 上で説明したように正弦波においては各点は単振動の動きをしますので、たとえば原点の変位(左図の赤玉の高さ)は、振幅を \(A\) 、角速度を \(ω\) としますと、
上で説明したように正弦波においては各点は単振動の動きをしますので、たとえば原点の変位(左図の赤玉の高さ)は、振幅を \(A\) 、角速度を \(ω\) としますと、
\(y = A\sinωt\)
と表せます。
波の周期が \(T\) であれば \(ω = {\large\frac{2π}{T}}\) であるので上式は
\(y = A\sin{\large\frac{2π}{T}}t\) ……①
とも表せます。
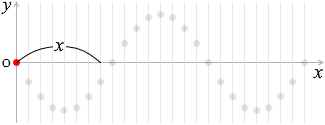 さらに、原点から \(x\) だけ離れた点の変位について考えてみますと、
さらに、原点から \(x\) だけ離れた点の変位について考えてみますと、
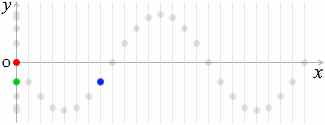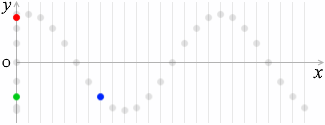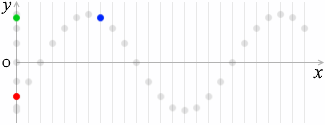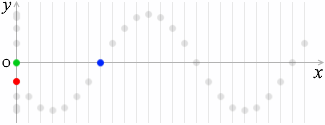 この点(青玉)の動きは緑玉の動きと同じであり、
この点(青玉)の動きは緑玉の動きと同じであり、
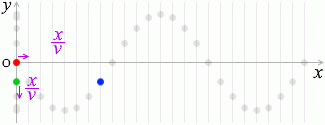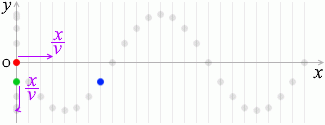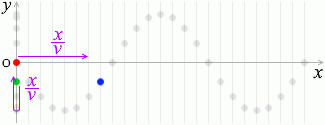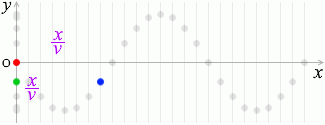 波の速さを \(v\) としますと、原点から \(x\) の点まで進むのに掛かる時間は \({\large\frac{x}{v}}\)秒であり
\({\large\frac{距離}{速さ}} = 時間\)
、これはつまり緑玉は赤玉から \({\large\frac{x}{v}}\)秒遅れているということであり、その変位は①式の \(t\) の部分に \(\big(t - {\large\frac{x}{v}}\big)\) を代入して、
波の速さを \(v\) としますと、原点から \(x\) の点まで進むのに掛かる時間は \({\large\frac{x}{v}}\)秒であり
\({\large\frac{距離}{速さ}} = 時間\)
、これはつまり緑玉は赤玉から \({\large\frac{x}{v}}\)秒遅れているということであり、その変位は①式の \(t\) の部分に \(\big(t - {\large\frac{x}{v}}\big)\) を代入して、
\(y = A\sin{\large\frac{2π}{T}}\big(t - {\large\frac{x}{v}}\big)\)
と表され、これが青玉の変位ということになります。
波の波長が \(λ\) であれば \(Tv = λ\) である
波の基本式
\(f = {\large\frac{1}{T}}\)
\(v = fλ\)
より、
\(v = {\large\frac{1}{T}}λ\)
∴ \(Tv = λ\)
ので、上式は
\(y = A\sin{\large\frac{2π}{T}}\big(t - {\large\frac{x}{v}}\big)\)
= \(A\sin2π\big({\large\frac{t}{T}} - {\large\frac{x}{Tv}}\big)\)
= \(A\sin2π\big({\large\frac{t}{T}} - {\large\frac{x}{λ}}\big)\)
とも書き表せます。
この式には \(x\) も \(t\) も含まれていますので、上で示した立体グラフのあらゆる地点の変位を表すことができます。
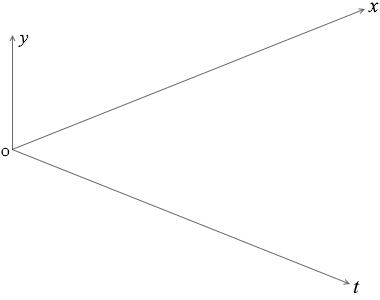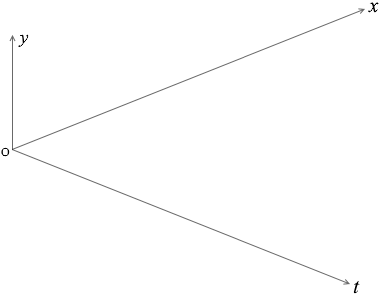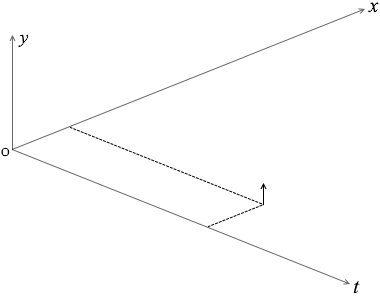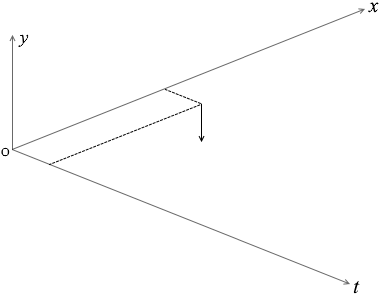
そして、もし \(x\) の値が \(x_1\) に固定されているとすれば、
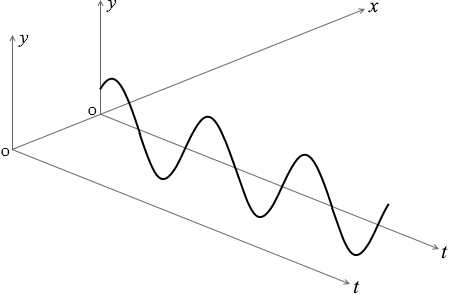 \(x_1\) の点の時間変化を表す式ということになりますし、
\(x_1\) の点の時間変化を表す式ということになりますし、
\(y = A\sin2π\big({\large\frac{t}{T}} - {\large\frac{x_1}{λ}}\big)\)
もし \(t\) の値が \(t_1\) に固定されているとすれば、
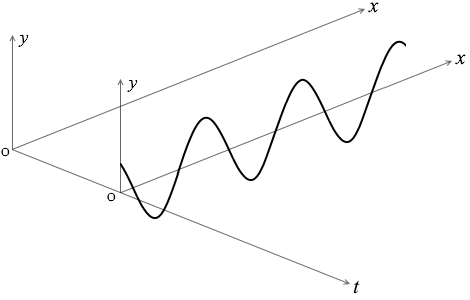 \(t_1\) の時刻の波の形を表す式ということになります。
\(t_1\) の時刻の波の形を表す式ということになります。
\(y = A\sin2π\big({\large\frac{t_1}{T}} - {\large\frac{x}{λ}}\big)\)
特殊な場合
正弦波を表す
\(y = A\sin{\large\frac{2π}{T}}\big(t - {\large\frac{x}{v}}\big)\)
= \(A\sin2π\big({\large\frac{t}{T}} - {\large\frac{x}{λ}}\big)\)
というこの式は
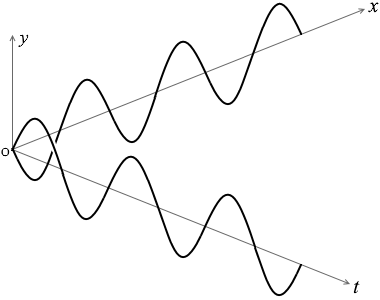 波が \(x\)軸の正の方向へ進み、原点の変位が、時刻 0 において 0 で、これから増えていく、というような場合の式ですが、
波が \(x\)軸の正の方向へ進み、原点の変位が、時刻 0 において 0 で、これから増えていく、というような場合の式ですが、
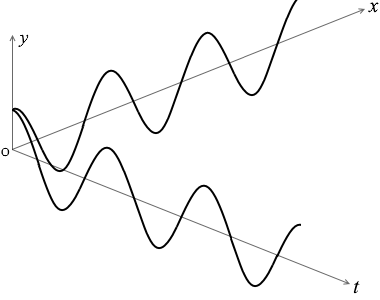 時刻 0 における原点の変位が波の頂点であるように定義されている場合は、
時刻 0 における原点の変位が波の頂点であるように定義されている場合は、
位相が \({\large\frac{π}{2}}\) 進んでいると考えられ、式は、\(\sin\) の中身に \({\large\frac{π}{2}}\) を足して
\(y = A\sin\Big\{{\large\frac{2π}{T}}\big(t - {\large\frac{x}{v}}\big)\) + \({\large\frac{π}{2}}\Big\}\)
\(= A\sin\Big\{2π\big({\large\frac{t}{T}} - {\large\frac{x}{λ}}\big)\) + \({\large\frac{π}{2}}\Big\}\)
となります。
また、
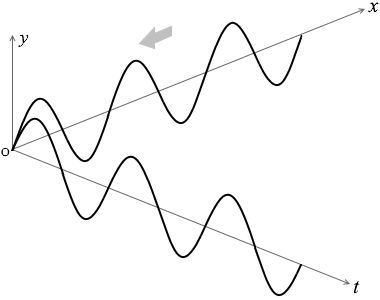 波の進行方向が \(x\)軸の正の方向ではなく負の方向であるような場合は、
波の進行方向が \(x\)軸の正の方向ではなく負の方向であるような場合は、
\(v\) の部分が \(- v\) となり、式は
\(y = A\sin{\large\frac{2π}{T}}\big(t + {\large\frac{x}{v}}\big)\)
\(= A\sin2π\big({\large\frac{t}{T}} + {\large\frac{x}{λ}}\big)\)
となります。
 物体が円周上を一定の速さでまわり続ける運動を等速円運動と呼びますが、この物体に横から光を当てると壁に映った影は周期的な往復運動をします。
物体が円周上を一定の速さでまわり続ける運動を等速円運動と呼びますが、この物体に横から光を当てると壁に映った影は周期的な往復運動をします。  この動きを単振動といいます。物理において等速直線運動の次に基本となる重要な運動です。
この動きを単振動といいます。物理において等速直線運動の次に基本となる重要な運動です。 各点が隣の点を引っ張っり上げたり引き下ろしたりしながら次々に伝わるのが波です。波をよく伝える媒質はばねの性質を持ち、各点がこの単振動という動きをしています。目を凝らして1つの縦の線に注目して見てください。
各点が隣の点を引っ張っり上げたり引き下ろしたりしながら次々に伝わるのが波です。波をよく伝える媒質はばねの性質を持ち、各点がこの単振動という動きをしています。目を凝らして1つの縦の線に注目して見てください。

 上で説明したように正弦波においては各点は単振動の動きをしますので、たとえば原点の
上で説明したように正弦波においては各点は単振動の動きをしますので、たとえば原点の さらに、原点から \(x\) だけ離れた点の変位について考えてみますと、
さらに、原点から \(x\) だけ離れた点の変位について考えてみますと、 この点(青玉)の動きは緑玉の動きと同じであり、
この点(青玉)の動きは緑玉の動きと同じであり、 波の速さを \(v\) としますと、原点から \(x\) の点まで進むのに掛かる時間は \({\large\frac{x}{v}}\)秒であり
波の速さを \(v\) としますと、原点から \(x\) の点まで進むのに掛かる時間は \({\large\frac{x}{v}}\)秒であり
 \(x_1\) の点の時間変化を表す式ということになりますし、
\(x_1\) の点の時間変化を表す式ということになりますし、 \(t_1\) の時刻の波の形を表す式ということになります。
\(t_1\) の時刻の波の形を表す式ということになります。 波が \(x\)軸の正の方向へ進み、原点の変位が、時刻 0 において 0 で、これから増えていく、というような場合の式ですが、
波が \(x\)軸の正の方向へ進み、原点の変位が、時刻 0 において 0 で、これから増えていく、というような場合の式ですが、 時刻 0 における原点の変位が波の頂点であるように定義されている場合は、
時刻 0 における原点の変位が波の頂点であるように定義されている場合は、 波の進行方向が \(x\)軸の正の方向ではなく負の方向であるような場合は、
波の進行方向が \(x\)軸の正の方向ではなく負の方向であるような場合は、