単スリット

単スリットによる光の干渉

ヤングの干渉実験、回折格子 において、スリットが2つの場合、多数の場合の光の干渉について説明しましたが、本項ではスリットが1つの場合の光の干渉について説明します。スリットが1つでは干渉しないのではないかと思われるかもしれませんが、実は干渉します。

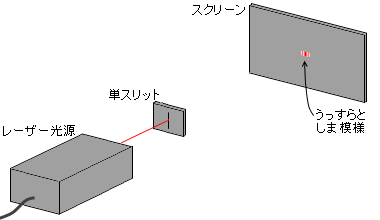左図のような装置において、単スリットのスリット幅がとても小さい場合、スクリーンに干渉縞が現れます。スリット幅が 1mm もあると、それは広すぎで、スクリーンにはただの点しか映りません。スリット幅を光の波長（5.0×10^-7m）の数倍程度まで細めると、光はわずかに横に広がり、うっすらと縞模様しまもようが現れます。

明線・暗線の条件

『ヤングの干渉実験』、『回折格子』と同じ要領で d と λ の関係を求めてみます。スリットの間に12個の素元波が等間隔にあるとみなします。

（dsinθ₁ = λ の場合。P₁）
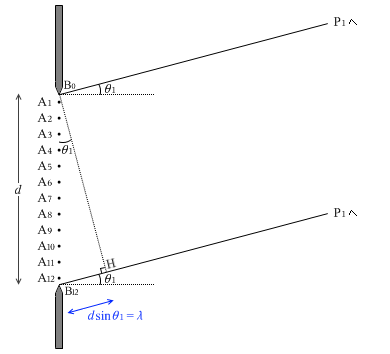左図のように、スリット幅を d とし、A₁～A₁₂の各点から素元波が出ているとみなします。いま、スリットの上端をB₀、スリットの下端をB₁₂、B₀からA₁の距離、A₁₂からB₁₂の距離はA₁からA₂の距離の半分とし、
　|B₀P₁ - B₁₂P₁| = λ
を満たすようなP₁と θ₁ を定めます。
|B₀P₁ - B₁₂P₁| というのは dsinθ₁ だから、つまり、
　dsinθ₁ = λ
となるようにP₁と θ₁ を定めるということです。

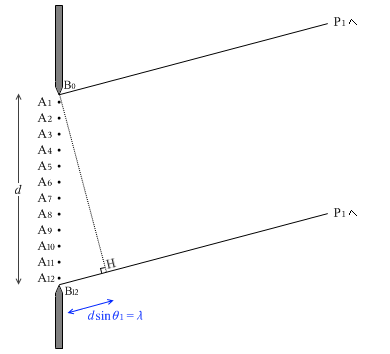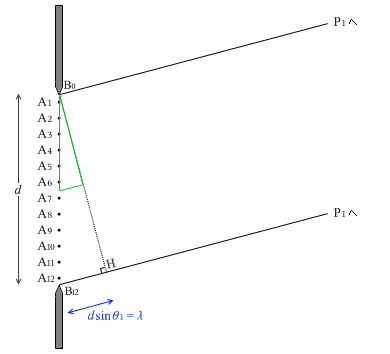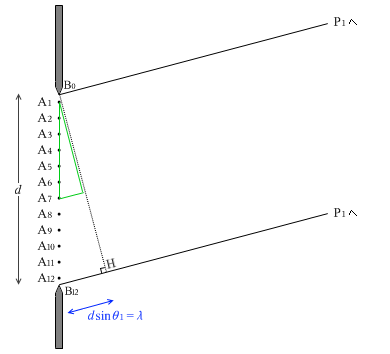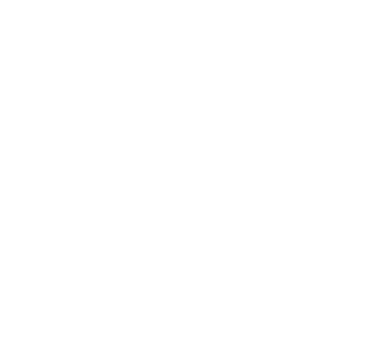A₁～A₁₂の各点からP₁に向かって素元波が出ているわけですが、ここで、△B₁₂B₀Hに比べ \(\large{\frac{1}{2}}\)の大きさの相似の△三角形を考えますと、この△三角形の底辺の長さは \(\large{\frac{1}{2}}\)λ です。この△三角形を下に少しズラすと、頂点がA₁とA₇と一致します。このことにより、
　|A₁P₁ - A₇P₁| = \(\large{\frac{1}{2}}\)λ
とわかります。

『ヤングの干渉実験』で説明したように、光路差 |A₁P₁ - A₇P₁| が \(\large{\frac{1}{2}}\)λ になるということは、A₁からの波とA₇からの波がP₁で打ち消し合って暗くなるということです。

同様にして、A₂とA₈、A₃とA₉、A₄とA₁₀、A₅とA₁₁、A₆とA₁₂が打ち消し合います。結局全部打ち消し合って、P₁は暗くなります。

つまり、dsinθ₁ = λ を満たすような点P₁は暗くなります。

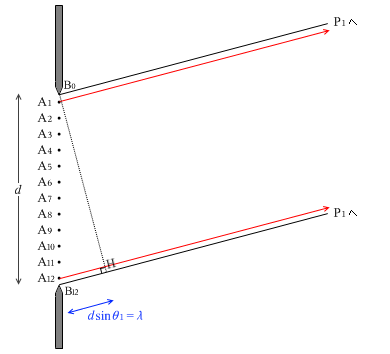ここで、A₁とA₁₂を見比べれば光路差がほぼ λ なのだから強め合ってP₁で明るくなるのではないかと思ってしまうかもしれません。が、そうはなりません。A₁の波の山とA₁₂の波の山がP₁で重なって大きな山ができそうですが、それと同時にA₆の波の谷とA₇の波の谷がP₁で重なって大きな谷ができるからです。結局大きな山と大きな谷が重なって打ち消し合います。同様にA₂、A₁₁、A₅、A₈の４つも打ち消し合い、A₃、A₁₀、A₄、A₉の４つも打ち消し合います。

つまり、どのような組み合わせで考えても、dsinθ₁ = λ のときは暗くなります。

（dsinθ₂ = \(\large{\frac{3}{2}}\)λ の場合。P₂）
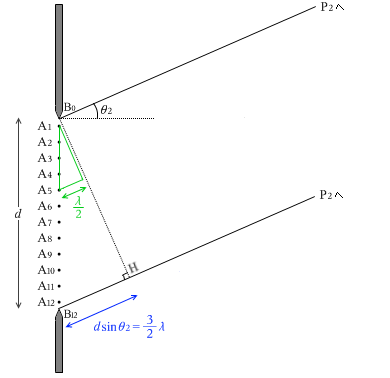次にもう少し角度をつけて、dsinθ₂ = \(\large{\frac{3}{2}}\)λ の場合を考えます。

今度は、△B₁₂B₀Hに比べ \(\large{\frac{1}{3}}\)の大きさの相似の△三角形を考えます。すると、この△三角形の底辺の長さは \(\large{\frac{1}{2}}\)λ です。この△三角形を下に少しズラすと、頂点がA₁とA₅と一致します。このことにより、
　|A₁P₂ - A₅P₂| = \(\large{\frac{1}{2}}\)λ
とわかります。つまり、A₁から出てP₂に達した波と、A₅から出てP₂に達した波は、互いに打ち消し合います。同様に、A₂とA₆、A₃とA₇、A₄とA₈も互いに打ち消し合います。そして、A₉、A₁₀、A₁₁、A₁₂が残ります。そして、P₂は、この残った４つの波によって明るくなります。

別のいい方をしますと、A₉、A₁₀、A₁₁、A₁₂が残るというよりも、
　A₁+A₅+A₉=山+谷+山=山
　A₂+A₆+A₁₀=山+谷+山=山
　A₃+A₇+A₁₁=山+谷+山=山
　A₄+A₈+A₁₂=山+谷+山=山
という感じです。

というわけで、dsinθ₂ = \(\large{\frac{3}{2}}\)λ を満たすような点P₂は明るくなります。

（dsinθ = 0 の場合。P₀）
θ = 0 の場合、つまりスリットの正面（P₀とします）に進んでいく波については、位相がズレるようなことはなく（例えばA₁から出た波が山ならA₂～A₁₂から出た波も山）、P₀は明るくなります。

（dsinθ = \(\large{\frac{1}{2}}\)λ の場合）
dsinθ = \(\large{\frac{1}{2}}\)λ の場合（P₀とP₁の中間）は、上の dsinθ₂ = \(\large{\frac{3}{2}}\)λ の場合と同様に考えていくと明るくなると分かるのですが、dsinθ = 0 の場合のP₀も明るくなるので、これと区別が付きません。「明、明、暗、明、暗、…」と並んでいると二番目の「明」は認識できません。

（一般化）
素元波の数が12個ではなく、もっとたくさんあるとみなすと話が複雑になってしまいますが、以下のように考えると分かりやすくなります。

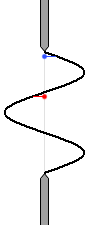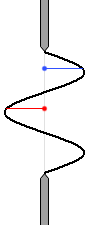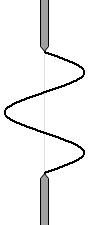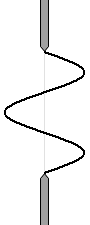波が打ち消し合うのは逆位相の波がぶつかるからであり、その位相を考えるために波を描いてしまいます。

左図の青点から出る波と赤点から出る波は位相が逆なので打ち消し合います。

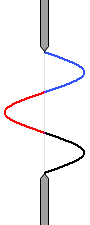打ち消し合わない黒い部分が残ればスクリーンは明るくなります。

左図は、上で説明した dsinθ = \(\large{\frac{3}{2}}\)λ の場合に相当します。

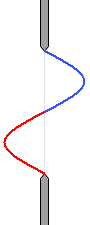黒い部分が残らなければスクリーンは暗くなります。

左図は、上で説明した dsinθ = λ の場合に相当します。

黒い部分がわずかしか残らなければスクリーンは少しだけしか明るくなりません。

左図は dsinθ = \(\large{\frac{5}{2}}\)λ の場合に相当します。

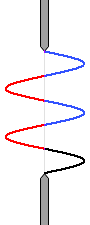
黒い部分がたっぷり残ればスクリーンはかなり明るくなります。

左図は dsinθ = \(\large{\frac{1}{2}}\)λ の場合に相当します。

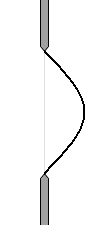
さらにもっと明るくなるのが左図のような場合です。
黒い部分は波が打ち消し合わないとはいえ、位相がズレていることに変わりはなく、多少の打ち消し合いは起こります。その多少の打ち消し合いが上の場合よりも左の場合の方が少ないです。位相のズレがほとんど無いからです。

dsinθ ≒ 0 の場合に相当します。P₀付近を照らす光です。

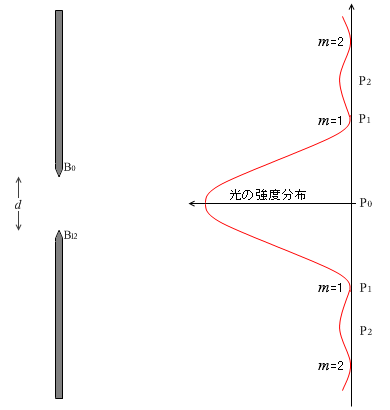というわけで単色光を単スリットに通し、スクリーンに当てたときの光の強度分布は左図のようになります。

以上まとめますと、回折格子の場合とほぼ逆になり、以下のようになります。

m は、「m = 0,1,2,…」ではなく、「m = 1,2,3,…」です。

回折格子と単スリットの競合

単スリットの条件式を回折格子の場合の条件式と見比べると、単スリットをたくさん連ねて回折格子を作った場合、dsinθ = λ を満たす点ではいったい明るくなるのか暗くなるのか？という疑問がわくかもしれません。回折格子の条件式の d はスリット間隔であり、単スリットの条件式の d はスリット幅であり違うものですが、双方の d が同じ値であるとき sinθ の値も同じになり、その角度が指す箇所では、回折格子の条件式に従えば明るくなるはずが、単スリットの条件式に従うと暗くなってしまいます。たとえばスリット幅が 0.1mm で、スリット間隔も 0.1mm の場合です。
このような場合はスリットから飛び出してくる光が暗いわけですからやっぱり暗くなります。
このようなことを防ぐためにはスリット幅を小さくしなければなりません。そうすれば sinθ の値が大きくなり（これは単スリットの条件式による sinθ です）、回折格子の条件式による sinθ の値と競合しなくなります。
ですから回折格子はスリット間隔よりスリット幅が小さいもののほうが性能がいいということになります。