光の屈折の法則
光も波動の一種なので屈折の法則（スネルの法則）が成り立っています。
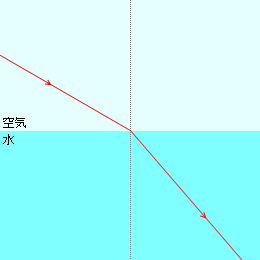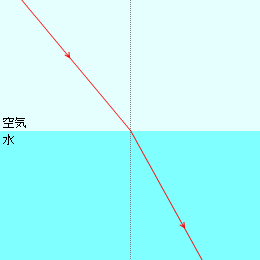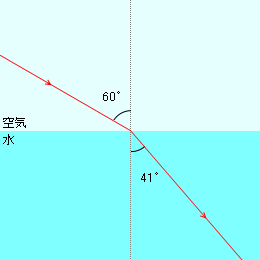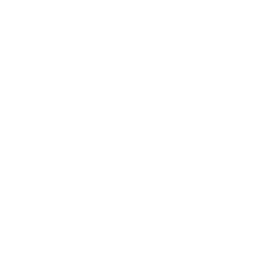左図は光が空気から水へ進む様子です。入射角の方が屈折角よりも大きいです。この様子は音波の場合と逆です。（”屈折の法則”の媒質2によって屈折角が変化するイラストも参照）
空気の中を進む光の速さや水の中を進む光の速さは決まっているので、入射角の正弦と屈折角の正弦の比も決まっています。
相対屈折率と絶対屈折率
相対屈折率
入射角を \(i\) 、屈折角を \(r\) 、媒質1における波の速さを \(v_1\) 、媒質2における波の速さを \(v_2\) としたとき、
\({\large\frac{\sin i}{\sin r}} = {\large\frac{v_1}{v_2}} = n_{12} =\) 一定 ……①
となり、\(n_{12}\) の値を相対屈折率（媒質1に対する媒質2の屈折率）という、と『屈折の法則』項で説明しましたが、
絶対屈折率
このとき特に、光波が真空から媒質aに進んだ場合の屈折率を絶対屈折率（真空に対する媒質aの屈折率）といい、\(n_{\rm a}\) 絶対屈折率は添え字が1個で、相対屈折率は添え字が2個です。 あるいは単に \(n\) と表します。
そしてややこしいのが、単に「屈折率」といった場合にはこれは「絶対屈折率」の方を指します。ですので相対屈折率を指す場合は「相対」を付けるのを忘れないようにします。もしくは長々と「媒質1に対する媒質2の屈折率」といいます。試験問題を解くときにはこれらのことに注意しなければなりません。あとちなみに、音波には絶対屈折率というものはありません。音波は真空の中を進めません。
①式にならって、
入射角を \(i'\) 、屈折角を \(r'\) 、真空における光速を \(c\) 、媒質aにおける光速を \(v_{\rm a}\) とすると、
\({\large\frac{\sin i'}{\sin r'}} = {\large\frac{c}{\ v_{\rm a}}} = n_{\rm a} =\) 一定 ……②
と書けます。
| 絶対屈折率 | 真空からその物質へ光が進むとき | |
|---|---|---|
| 空気 | 1.0003 | ほとんど曲がらない |
| 水 | 1.3330 | 一番上の図と同じ感じ |
| ガラス | 1.4585 | 水のときより曲がる |
| ダイヤモンド | 2.4195 | ものすごく曲がる |
空気の絶対屈折率は真空と同じ、とする場合が多いです。
絶対屈折率が大きい媒質は光速が遅いということです。各媒質での光速は、②式より以下のように表せます。
媒質aでの光速
\(\boldsymbol{v_{\rm a} = {\large\frac{c}{\ n_{\rm a}}}}\)
たとえば、水における光速は真空中の光速を水の絶対屈折率で割れば導き出せます。
\(v_水 = {\large\frac{c}{\ n_水}} = {\large\frac{3.0\times10^8}{\ 1.3330}} ≒ 2.3×10^8\) [m/s]
相対屈折率と絶対屈折率の関係
上式より、
媒質1での光速は、
\({\color{red}v_1 = {\large\frac{c}{\ n_1}}}\)
媒質2での光速は、
\({\color{blue}v_2 = {\large\frac{c}{\ n_2}}}\)
であるので、媒質1から媒質2へ進むときの相対屈折率 \(n_{12}\) は、
\(n_{12} = {\large\frac{v_1}{v_2}} = {\large\frac{\color{red}{v_1}}{\color{blue}{v_2}}} = {\Large\frac{\color{red}{\frac{c}{\ n_1}}}{\color{blue}{\frac{c}{n_2}}}} = {\Large\frac{\frac{1}{\ n_1}}{\frac{1}{n_2}}} = {\large\frac{n_2}{n_1}}\)
となります。\(v\) と \(n\) では分母分子が逆転しています。
相対屈折率と絶対屈折率の関係
\(\boldsymbol{n_{12} = {\large\frac{n_2}{n_1}}}\)
たとえば、この式から、水からガラスに光が進むときの相対屈折率がわかります。上の表で示したそれぞれの絶対屈折率を当てはめますと、
\(n_{水ガラス} = {\large\frac{n_{ガラス}}{n_水}} = {\large\frac{1.4585}{\ 1.3330}} ≒ 1.094\)
とわかります。
また、\(n_{12} = {\large\frac{n_2}{n_1}}\) を①式に代入すると、
\({\large\frac{\sin i}{\sin r}} = n_{12} = {\large\frac{n_2}{n_1}}\)
この式は一番上で示した、
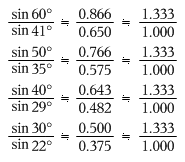
のことを表しています。
であるので、
\(n_1\sin i = n_2\sin r\)
という関係もあることがわかります。
覚え方
\(n_{12} = {\large\frac{n_2}{n_1}}\) という分数の式を見て、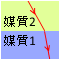
と想像してはいけません。あくまでも先に通る方が分母で、後に通る方が分子です。正解は 
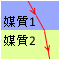もしくは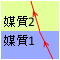 
です。この式は 
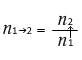と矢印を付与して覚えてください。
それから、「媒質1に対する媒質2の屈折率」という日本語の表現ですが、これは先に媒質1を通って後に媒質2を通るときの屈折率という意味です。「媒質」というのは「物質」のことです。（『相対速度』項も参照）
屈折率関連の式は覚えにくいので矢印を付与して覚えてください。
”波の屈折”の項の最後に示した式
\({\large\frac{\sin i}{\sin r}} = {\large\frac{v_1}{v_2}}\) = \({\large\frac{\lambda_1}{\lambda_2}} = n_{12} =\) 一定
と共に確実に覚えてください。