氷の上で石を滑らせることについて考えよう。はじめ、図1のように、質量 M の人が質量 m の石とともに、速度 V0 で摩擦のない水平な氷の上を滑っている。ただし、すべての運動は一直線上で起こるとし、図1・図2の右向きを正の向きとする。
（問1）人が一定の力 F を時間 Δt の間だけ加えて石を水平に押したところ、図2のように、人と石は互いに離れて、人の速度は V 、石の速度は v となった。V と v はそれぞれいくらか。
（問2）問1で石が人の手を離れたとき、人がちょうど静止した。この場合、人と石の運動エネルギーの合計は、石を押した後には、押す前に比べて何倍になったか。
（問3）qG7FA
#センター00本試
（問1）人が一定の力 F を時間 Δt の間だけ加えて石を水平に押したところ、図2のように、人と石は互いに離れて、人の速度は V 、石の速度は v となった。V と v はそれぞれいくらか。
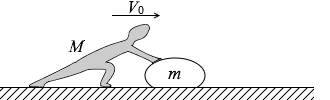
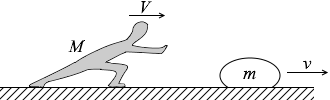
（題意がイメージしにくい方は、まず、『物体の分裂』項をお読みください。）
人についての運動量と力積の関係式（ mv' - mv = FΔt ）を立てますと、
MV - MV0 = - FΔt
∴ V - V0 = - \(\large{\frac{F}{M}}\)Δt
∴ V = V0 - \(\large{\frac{F}{M}}\)Δt ……①
石についての運動量と力積の関係式を立てますと、
mv - mV0 = FΔt
∴ v - V0 = \(\large{\frac{F}{m}}\)Δt
∴ v = V0 + \(\large{\frac{F}{m}}\)Δt ……②
人は \(\large{\frac{F}{M}}\)Δt だけ減速して、石は \(\large{\frac{F}{m}}\)Δt だけ加速します。
（問2）問1で石が人の手を離れたとき、人がちょうど静止した。この場合、人と石の運動エネルギーの合計は、石を押した後には、押す前に比べて何倍になったか。
石を押す前の、人と石の運動エネルギーの合計は
\(\large{\frac{1}{2}}\)(M + m)V02 ……③
石を押した後の、人と石の運動エネルギーの合計は
\(\large{\frac{1}{2}}\)⋅M⋅02 + \(\large{\frac{1}{2}}\)mv2
=\(\large{\frac{1}{2}}\)mv2 ……④
（③と④を比べるために、v を V0 で表します）
①式 V = V0 - \(\large{\frac{F}{M}}\)Δt に V = 0 を代入すると、
0 = V0 - \(\large{\frac{F}{M}}\)Δt
∴ \(\large{\frac{F}{M}}\)Δt = V0
∴ FΔt = MV0
これを②式 v = V0 + \(\large{\frac{F}{m}}\)Δt に代入すると、
v = V0 + \(\large{\frac{M}{m}}\)V0
∴ v = (1 + \(\large{\frac{M}{m}}\))V0
∴ v = \(\large{\frac{M+m}{m}}\)V0
（v を V0 で表せたので、これを④式 \(\large{\frac{1}{2}}\)mv2 に代入します）
④ = \(\large{\frac{1}{2}}\)m\(\big(\large{\frac{M+m}{m}}\big)\)2V02 ……④'
（③と④'を比べますと）
\(\large{\frac{④'}{③}}\) = \(\large{\frac{\frac{1}{2}m(\frac{M+m}{m})^2V_0^2}{\frac{1}{2}(M+m)V_0^2}}\) = \(\large{\frac{m(\frac{M+m}{m})^2}{(M+m)}}\) = \(\large{\frac{M+m}{m}}\)
（この式を吟味してみますと）
M ≫ m つまり人の体重が重くて石が軽いとき、運動エネルギーは何倍にもなり、
M ≪ m つまり人の体重が軽くて石が重いとき、運動エネルギーはちょっとしか増えない、
といえます。
言い換えますと、
人が重くて石が軽いときは、止まるためには多くの労力が必要で、
人が軽くて石が重いときは、止まるためにはそれほど労力は必要無い、
となります。