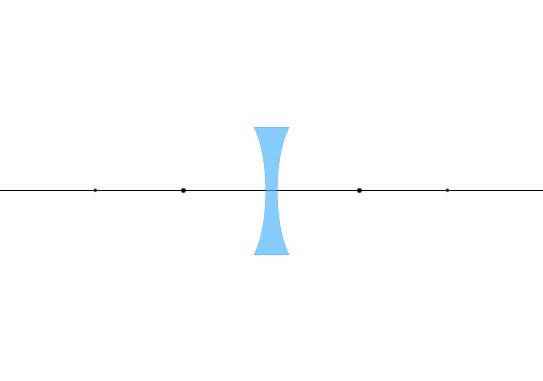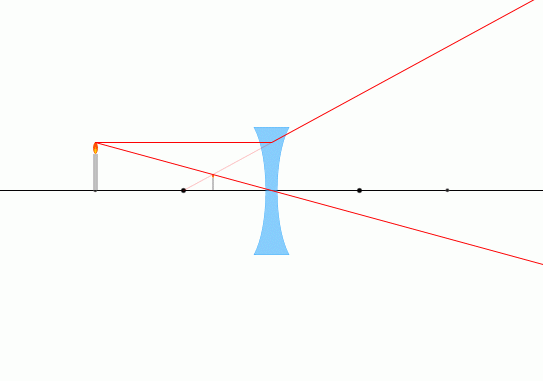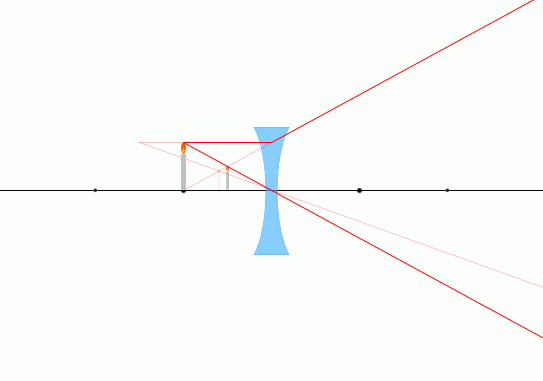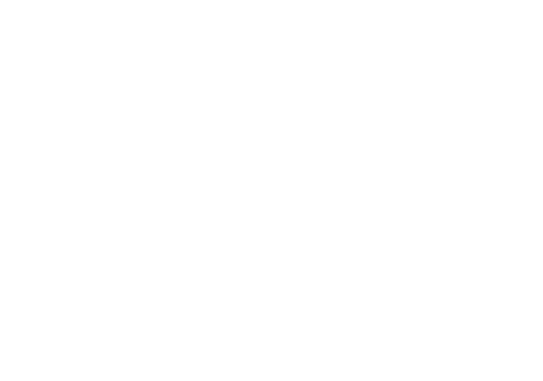凹レンズ

3つの量の関係を求める

凸レンズの場合と同じように、凹レンズにおける

　　物体とレンズとの距離：a
　　レンズと像との距離：b
　　焦点距離：f

の関係を考えてみます。

凹レンズのつくる像

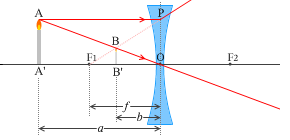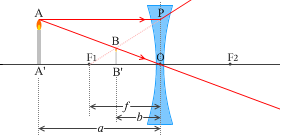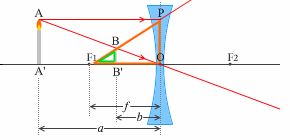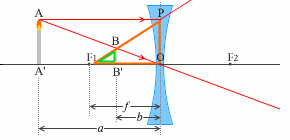左図にように、物体から凹レンズまでの距離を a 、凹レンズから像までの距離を b 、凹レンズの焦点距離を f とします。

左図の赤線は、レンズによる像（凹レンズ） の（1）、（2）にのっとった線です。（3）にのっとった線は必要ないので描いてません。

△AA'O と △BB'O は相似だから、

　　　　\(\color{#b63}{\large{\rm{\frac{BB'}{AA'}}}}\) = \(\large{\rm{\frac{B'O}{A'O}}}\) = \(\large{\frac{b}{a}}\)　　……①

また、AA'=PO であり、△POF₁ と △BB'F₁ が相似であるから、

　　　　\(\color{#b63}{\large{\rm{\frac{BB'}{AA'}}}}\) = \(\large{\rm{\frac{BB'}{PO}}}\) = \(\large{\rm{\frac{B'F_1}{OF_1}}}\) = \(\large{\frac{f\ -\ b}{f}}\)

よって、

　　　　\(\large{\frac{b}{a}}\) = \(\large{\frac{f\ -\ b}{f}}\)

　　　　 　 = 1 - \(\large{\frac{b}{f}}\)　　　（両辺を b で割って）

　∴　　\(\large{\frac{1}{a}}\) = \(\large{\frac{1}{b}}\) - \(\large{\frac{1}{f}}\)

　∴　　\(\large{\frac{1}{a}}\) - \(\large{\frac{1}{b}}\) = - \(\large{\frac{1}{f}}\)　　……②

f > 0 であるから上式の右辺は負でありすなわち左辺も負。

　　　　\(\large{\frac{1}{a}}\) - \(\large{\frac{1}{b}}\) < 0

　∴　　\(\large{\frac{1}{a}}\) < \(\large{\frac{1}{b}}\)　　　（b > 0 であるから）

　∴　　\(\large{\frac{b}{a}}\) < 1

m = \(\large{\frac{b}{a}}\) であるので、すなわち m < 1 、つまり、倍率が常に 1.0 より小さい、ということです。凹レンズでは像が常に縮小されるのです。拡大鏡としては使えません。

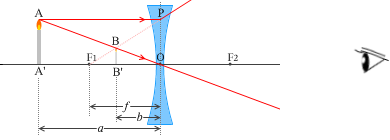凹レンズの場合は、物体を焦点より近くに置いても遠くに置いても、正立像の虚像（BB'）ができます。（前項の凸レンズの場合に比べれば単純です。）

凸レンズの式と凹レンズの式はまとめられる

前項の凸レンズにおいて、②式と④式をまとめて⑤式とすることができましたが、さらにこの⑤式は本項の②式と統合させることができます。⑤式において b と f を負としたものが、本項の②式である、と考えるのです。

＊ b と f が正の値のみをとると定めた場合に、

　　\(\large{\frac{1}{a}}\) + \(\large{\frac{1}{\color{blue}{b}}}\) = \(\large{\frac{1}{\color{blue}{f}}}\)　　……前項②　凸レンズ、焦点より遠く

　　\(\large{\frac{1}{a}}\) - \(\large{\frac{1}{\color{blue}{b}}}\) = \(\large{\frac{1}{\color{blue}{f}}}\)　　……前項④　凸レンズ、焦点より近く

　　\(\large{\frac{1}{a}}\) - \(\large{\frac{1}{\color{blue}{b}}}\) = - \(\large{\frac{1}{\color{blue}{f}}}\)　　……本項②　凹レンズ

となるこの3パターンを統合するということです。
　 閉じる

（レンズ後方とは、物体から見てレンズの向こう側。レンズ手前とは、物体から見てレンズのこちら側。）

表にまとめてみます