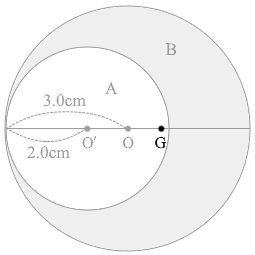
 物体Bの重心であるGの位置については直観的に点Oの 右側 とわかると思います。左側ということはありえません。
物体Bの重心であるGの位置については直観的に点Oの 右側 とわかると思います。左側ということはありえません。
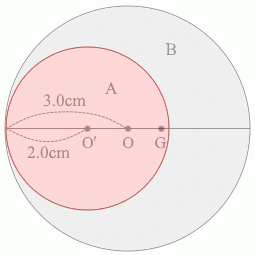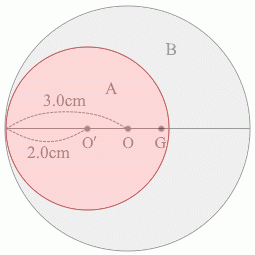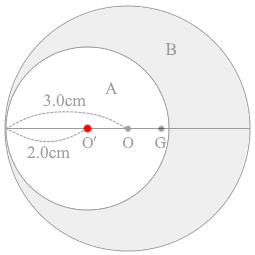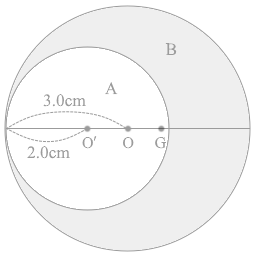 物体Aについて考えてみますと、その重心は点O'であるわけですが、仮に円盤が 1cm2 あたり 1kg の質量であったとすると物体Aの質量は 2.0×2.0×\(π\) = 4.0\(π\) [kg] であり
円の面積 \(πr^2\)
、重心について考えるときに、点O'に 4.0\(π\) kg の質量のものがあるとみなすことができます。
物体Aについて考えてみますと、その重心は点O'であるわけですが、仮に円盤が 1cm2 あたり 1kg の質量であったとすると物体Aの質量は 2.0×2.0×\(π\) = 4.0\(π\) [kg] であり
円の面積 \(πr^2\)
、重心について考えるときに、点O'に 4.0\(π\) kg の質量のものがあるとみなすことができます。
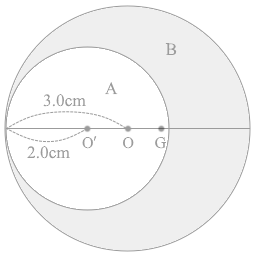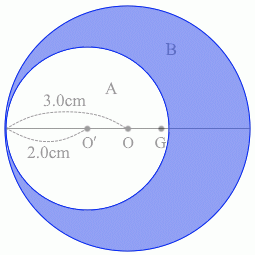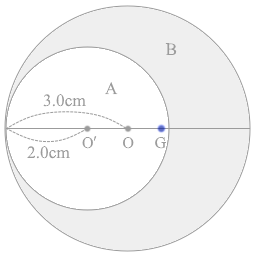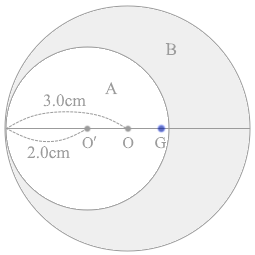 同様に物体Bについて考えてみますと、その面積は 3.0×3.0×\(π\) - 2.0×2.0×\(π\) = 9.0\(π\) - 4.0\(π\) = 5.0\(π\) であり、質量は 5.0\(π\) kg ということになり、点Gに 5.0\(π\) kg の質量のものがあるとみなせます。
同様に物体Bについて考えてみますと、その面積は 3.0×3.0×\(π\) - 2.0×2.0×\(π\) = 9.0\(π\) - 4.0\(π\) = 5.0\(π\) であり、質量は 5.0\(π\) kg ということになり、点Gに 5.0\(π\) kg の質量のものがあるとみなせます。
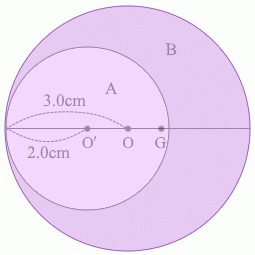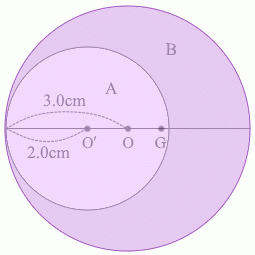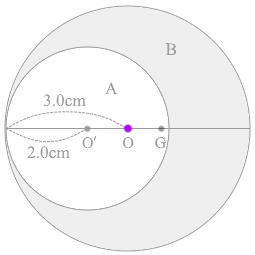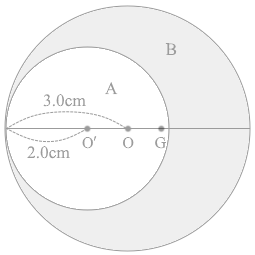 物体Aと物体Bが合わさると元の円盤になるわけですが、その重心は点Oであるわけなので、
物体Aと物体Bが合わさると元の円盤になるわけですが、その重心は点Oであるわけなので、
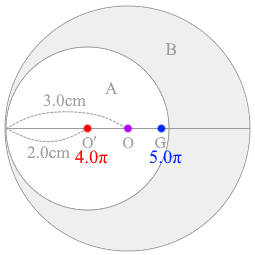 点O'にある 4.0\(π\) kg の物体と点Gにある 5.0\(π\) kg の物体の2つの物体の重心が点Oの位置である、ということになります。
点O'にある 4.0\(π\) kg の物体と点Gにある 5.0\(π\) kg の物体の2つの物体の重心が点Oの位置である、ということになります。
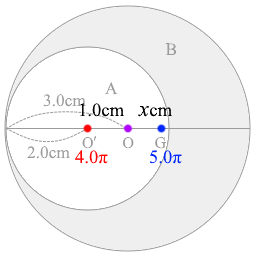 天秤を想像して暗算でOG間の距離(\(x\) とおく)を導き出しますと、回転軸からの距離は重さの逆比だから、
天秤を想像して暗算でOG間の距離(\(x\) とおく)を導き出しますと、回転軸からの距離は重さの逆比だから、
\(4.0π : 5.0π = x : 1.0\)
∴ \(x\) = 0.8 [cm]
重心の位置の式を立てて求めるとすれば、点Oを原点として
\(0 = \large\frac{4.0π(-1.0)\ +\ 5.0πx}{4.0π\ +\ 5.0π}\)
∴ \(0 = -4.0\ +\ 5.0x\)
∴ \(5.0x = 4.0\)
∴ \(x = 0.8\)
もし左端を原点として式を立てるなら
\(3.0 = \large\frac{4.0π×2.0\ +\ 5.0π(3.0+x)}{4.0π\ +\ 5.0π}\)
∴ \(27 = 8 + 15 + 5x\)
∴ \(5x = 27 - 23\)
∴ \(x = 0.8\)
となります。
答えは ② です。
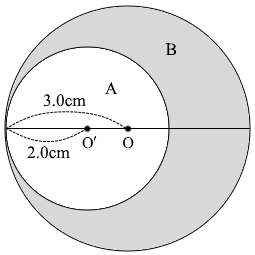
 物体Bの重心であるGの位置については直観的に点Oの 右側 とわかると思います。左側ということはありえません。
物体Bの重心であるGの位置については直観的に点Oの 右側 とわかると思います。左側ということはありえません。 物体Aについて考えてみますと、その重心は点O'であるわけですが、仮に円盤が 1cm2 あたり 1kg の質量であったとすると物体Aの質量は 2.0×2.0×\(π\) = 4.0\(π\) [kg] であり
物体Aについて考えてみますと、その重心は点O'であるわけですが、仮に円盤が 1cm2 あたり 1kg の質量であったとすると物体Aの質量は 2.0×2.0×\(π\) = 4.0\(π\) [kg] であり 同様に物体Bについて考えてみますと、その面積は 3.0×3.0×\(π\) - 2.0×2.0×\(π\) = 9.0\(π\) - 4.0\(π\) = 5.0\(π\) であり、質量は 5.0\(π\) kg ということになり、点Gに 5.0\(π\) kg の質量のものがあるとみなせます。
同様に物体Bについて考えてみますと、その面積は 3.0×3.0×\(π\) - 2.0×2.0×\(π\) = 9.0\(π\) - 4.0\(π\) = 5.0\(π\) であり、質量は 5.0\(π\) kg ということになり、点Gに 5.0\(π\) kg の質量のものがあるとみなせます。 物体Aと物体Bが合わさると元の円盤になるわけですが、その重心は点Oであるわけなので、
物体Aと物体Bが合わさると元の円盤になるわけですが、その重心は点Oであるわけなので、 点O'にある 4.0\(π\) kg の物体と点Gにある 5.0\(π\) kg の物体の2つの物体の重心が点Oの位置である、ということになります。
点O'にある 4.0\(π\) kg の物体と点Gにある 5.0\(π\) kg の物体の2つの物体の重心が点Oの位置である、ということになります。 天秤を想像して暗算でOG間の距離(\(x\) とおく)を導き出しますと、回転軸からの距離は重さの逆比だから、
天秤を想像して暗算でOG間の距離(\(x\) とおく)を導き出しますと、回転軸からの距離は重さの逆比だから、