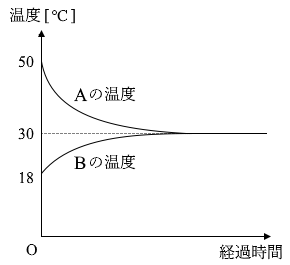
熱容量が \(C_{\rm A}\) = 3.0×102 J/K で温度が 50℃ の物体Aと、熱容量が \(C_{\rm B}\) で 温度が 18℃ の物体Bを接触させた。それぞれの温度変化を測定したところ。図4のようなグラフが得られた。十分長い時間が経った後、両者の温度は 30℃ になった。物体Aが物体Bに与えた熱量と、\(C_{\rm A}\) と \(C_{\rm B}\) の大小関係の組合せとして最も適当なものを、下の①~⑨のうちから一つ選べ。ただし、\(C_{\rm A}\) と \(C_{\rm B}\) は温度によらずそれぞれ一定で、物体Aと物体Bの間でのみ熱の移動があったものとする。
| 熱量 [J] | 大小関係 | |
|---|---|---|
| ① | 1.5 × 10 | \(C_{{\rm A}} > C_{\rm B}\) |
| ② | 1.5 × 10 | \(C_{{\rm A}} = C_{\rm B}\) |
| ③ | 1.5 × 10 | \(C_{{\rm A}} < C_{\rm B}\) |
| ④ | 3.6 × 103 | \(C_{{\rm A}} > C_{\rm B}\) |
| ⑤ | 3.6 × 103 | \(C_{{\rm A}} = C_{\rm B}\) |
| ⑥ | 3.6 × 103 | \(C_{{\rm A}} < C_{\rm B}\) |
| ⑦ | 6.0 × 103 | \(C_{{\rm A}} > C_{\rm B}\) |
| ⑧ | 6.0 × 103 | \(C_{{\rm A}} = C_{\rm B}\) |
| ⑨ | 6.0 × 103 | \(C_{{\rm A}} < C_{\rm B}\) |
#センター18本試物理基礎