電気力線

電気力線とは

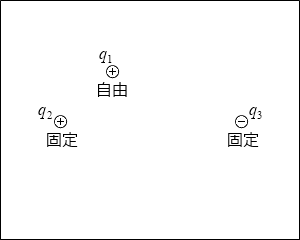q₁ 、q₂ 、q₃ の３つの電荷があるとします。

q₁ は正の電荷を持ち自由に動ける、q₂ は正の電荷を持ち固定されている、q₃ は絶対値が q₂ と同じで負の電荷を持ち固定されている、とします。

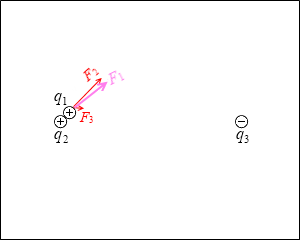始めに左図のような位置にいた q₁ は、クーロンの法則により、q₂ と q₃ から左図のような F₂ 、F₃ の静電気力を受けます。そして静電気力は足し合わせることができるので左図の F₁ のような力になります。つまり q₁ は F₁ の方向へ動きます。

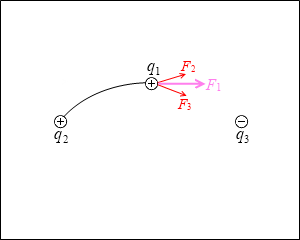すると今度は、左図のような F₂ 、F₃ の力を受け、結局、その合力である F₁ の方向へ動きます。

だんだん F₂ の大きさは小さくなっていき、F₃ の大きさは大きくなっていきます。

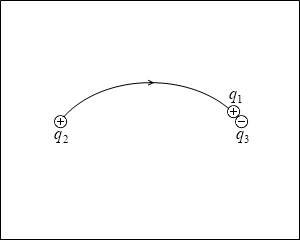そのように動いていって最後に q₃ の位置にたどり着きます。

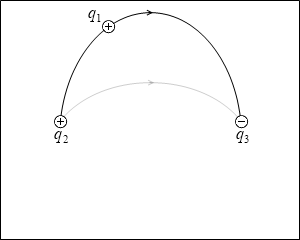もしスタート位置が q₂ の真上付近だった場合には、左図のように動いていきます。

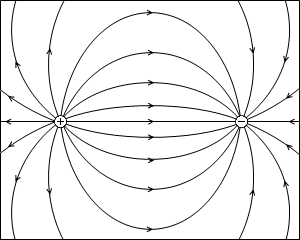そして、あらゆる位置からスタートした場合を描き込むと左図のようになります。

この軌跡を電気力線（でんきりきせん）といいます。仮想的な線です。自由に動ける正電荷 q₁ が動く方向であり、静電気力のはたらく方向であり、電場の方向、であります。

電気力線の例

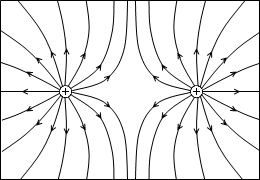q₂ も q₃ も正だった場合は左図のようになります。

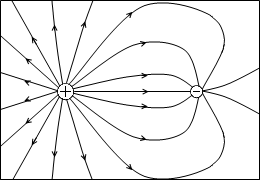q₂ の絶対値が q₃ の2倍で正で、q₃ が負だった場合。

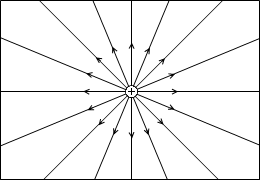q₂ のみだった場合。

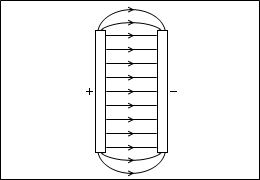q₂ 、q₃ の形状が板状だった場合。

電気力線の性質

1. 電気力線は正電荷から出て負電荷に入る。＊電荷が無くても、磁場が変化するときには電場が発生します。つまり、電荷が無いのに電気力線を描くことができます。そのときは必ず電気力線はループ状（閉曲線）になります。閉曲線には始まりと終わりが無いので 1. の条件に反していないといえます。へりくつですが…。
　閉じる

2. 電気力線は途切れたり急に始まったりしない。

3. 電気力線は交わったり枝分かれしたりしない。＊上で説明したように、静電気力は足し合わせることができるので F₂ と F₃ は必ず１つの方向（F₁）にまとめることができます。つまり電気力線は常に1本道です。
　閉じる

4. 電場の強さが E [N/C] の場所に 1m² 当たり E 本の密度で電気力線を描くことにすると、電場の強さを電気力線の密度で表現できる（下参照）。＊（細かい話なんですが、以下のことを頭に入れておいてください）
電場というものは3次元的に分布していて、つまり電気力線も3次元的に分布しています。これをイラストで表現すると、2次元になってしまい、これはある一つの断面を表しているだけ、ということになります。
たとえば点電荷の電場は、「距離の2乗に反比例」であるはずが、2次元イラストでは「距離に反比例」になってしまいます。イラストでは、距離が「倍」離れた地点の電気力線の密度が「半分」に見えてしまいます。本当は「1/4」です。ですから、もしイラストにおいて電場の強さを矢印で示すときは、「倍」離れた位置の矢印の長さは「半分」でなく「1/4」にして表現しなければなりません。
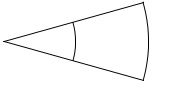2次元では、半径が2倍になると円弧の長さも2倍。
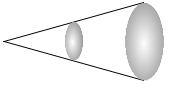3次元では、半径が2倍になると球弧の面積は4倍。

『逆2乗の法則』項もご参照ください。
　閉じる

ガウスの法則

始点と終点がある線分をある領域が取り囲むとき、領域の境界での線分の出入りの総計をカウントすると領域内部の始点と終点の総和が予想できます。このことをガウスの定理といいます。物理の分野では特にガウスの法則といいます。

分かりにくいと思うのでもう一度言い直します。

+ の端点から始まって - の端点で終わる線分がいくつかあって、端点をある閉曲面が囲むとき、閉曲面（境界面）を貫く線分を数えると、閉曲面内に存在する端点の総和が分かる、ということです。線分は途中で途切れたり枝分かれしないものとします。

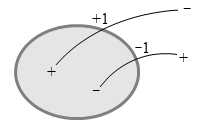このとき、出ていく線分は +1本とカウントし、入っていく線分は -1本とカウントします。

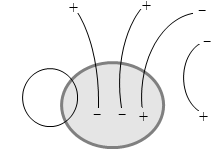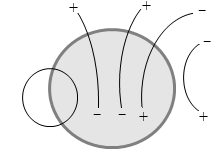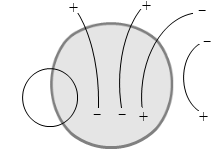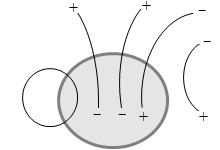
左図では、閉曲面内の端点は + が1個と - が1個で総計 0 個です。

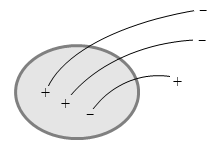左図の例では、出ていく線分は +2本で、入っていく線分は -1本で総計 +1本です。閉曲面内には端点が総計 +1個存在すると分かります。

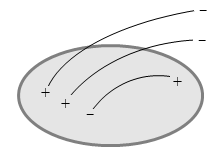左図の例では、出ていく線分は +2本で、入っていく線分は 0本で総計 +2本です。閉曲面内には端点が総計 +2個存在すると分かります。

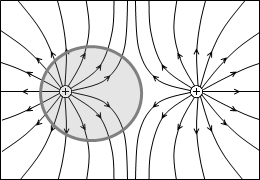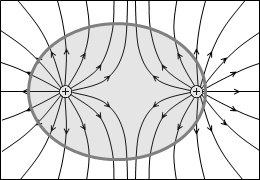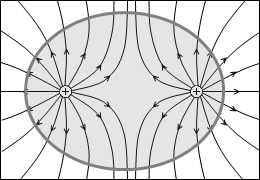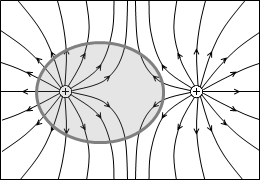
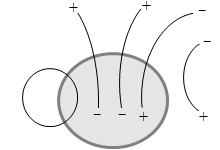左図の例では、出ていく線分は +2本で、入っていく線分は -3本で総計 -1本です。閉曲面内には端点が総計 -1個存在すると分かります。

ループ状の電気力線は出入りがそれぞれ1回ずつで、どちらかが「入り」でどちらかが「出」です。ループ状の電気力線は特別な場合にしか発生しません。

そもそもループ状の線をカウントせず、出ていく線分は +1本で、入っていく線分は -2本で総計 -1本、と考えてもいいです。

ガウスの法則においては、その閉曲面の形はどのような形でもかまいません。大きくても小さくてもいびつな形でも、閉曲面を貫く本数が変わらなければ閉曲面内の端点の数も変わりません。これはガウスの法則の大きな特徴です。

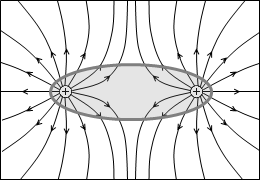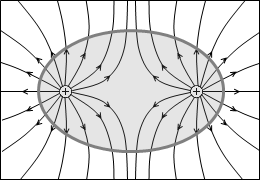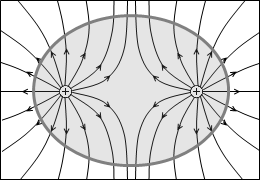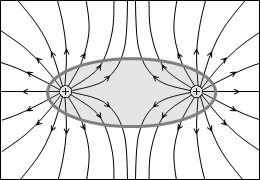上で示した電気力線の例で説明しますと、電荷を覆う閉曲面を貫く電気力線の本数が変わらなければ内部の電荷の量も変わりません。

左図の場合は、閉曲面を貫く電気力線の本数が変わってしまうので内部の電荷の量は変わります。

以上がガウスの法則の原則なのですが、電気力線というものは一般に、電場の方向に垂直な断面を通る本数、として定義されますので、電場から電荷を求めたり、電荷から電場を求めたりする際には、電気力線を垂直に横切るような面からなる閉曲面を考えて、その形の閉曲面で電荷を囲むようにします。そうでないと正確な電気力線の本数を割り出せません。点電荷でしたら球面を考え、棒状電荷なら円柱を考えたりします。

電荷におけるガウスの法則

+q [C] の点電荷からは、いったい何本の電気力線が出ているか、考えてみます。電場の強さが E [N/C] の場所では、電場の方向に垂直な 1m² の断面に E 本 の電気力線が通るものとします。

電荷を中心とした半径 r の球面を考え＊このとき、できれば、半径が 0.282m の球面（表面積がちょうど 1m² になる球）を考えてしまうと、計算が早いです。ちょっと考え方が難しいですが…。
　 閉じる、この球面を何本の電気力線が通るかを求めれば、これが +q [C] から出る電気力線の本数です。

点電荷のまわりでは電場の強さは　E = \(k\large{\frac{q}{r^2}}\) [N/C]　であり、これは半径 r のこの球面の位置での電場の強さのことです。

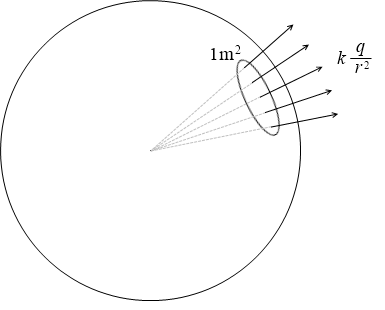といういことは 1m² 当たり E 本、つまり \(k\large{\frac{q}{r^2}}\) 本の電気力線が通っているということです。

球面の面積は 4πr² [m²] ですから、球面全体を貫く電気力線の本数は

　　4πr² × \(k\large{\frac{q}{r^2}}\) = 4πkq [本]

と分かります。

ガウスの法則によれば、この球面はどんな大きさであっても 4πkq 本です。（そもそも r が含まれていないことがそのことを示唆しています）。また点電荷でなくて、大きさと形がある電荷であっても 4πkq 本です。

このガウスの法則を用いて、電荷から電場を求めたり、電場から電荷を求めたりすることができます。Q が負のときは本数も負になってしまいますが、そのときは、外から内に向かう電気力線の本数、と解釈します。正のときは湧き出しの本数で、負のときは吸い込みの本数です。あと、電気力線の本数は整数というわけではありません。電気力線は人間が決めた仮想のものですし、たとえ0.53本なんておかしいと思っても、それなら定義を「1m²当たりE本」というところを「1m²当たりE×100本」と変えてしまえばいいだけです。

ちなみに、Q が +1 C の場合を考えてみますと、電気力線の本数は 4πk 本。この電荷が真空中にあるとすると、k = k₀ = 9.0×10⁹ だから、4πk ≒ 4×3.14×9.0×10⁹ = 1.13×10¹¹ 本、ということになります。