相互誘導

相互誘導とは

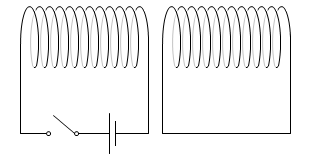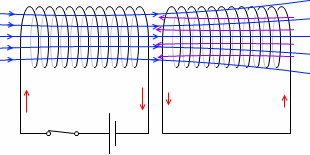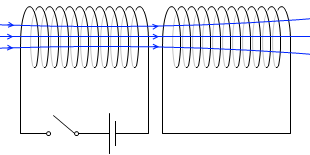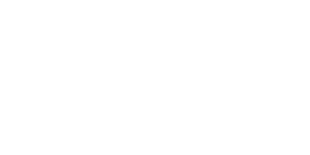コイルを含む回路が2つあるとします。左の回路には電源が付いてますが、右の回路には電源がありません。

左の回路（1次コイル）のスイッチを閉じると電流が流れ、コイル内部に磁場が発生します。右の回路（2次コイル）の位置があまり離れてなければ、1次コイルの磁場が2次コイルに影響を与えます。

1次コイルの電流が一定なら何も起こりませんが、もし電流が変化すると、1次コイル内の磁場が変化し、その影響で2次コイルにおいて電磁誘導が起こります。電源の無いはずの右の回路に電流が流れるのです。この現象を相互誘導といいます。

スイッチを開いた瞬間にも相互誘導は起こります。スイッチを閉じるときと開くときでは、2次コイルに流れる電流の方向は逆になります。

鉄心

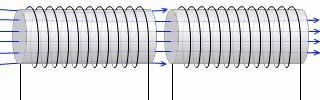2次コイルに起こす起電力を大きくするためには、鉄心を用いた方がいいです。透磁率 μ が大きい方が磁束密度 B が大きくなり、磁束 Φ が大きくなり、起電力 V が大きくなるからです。

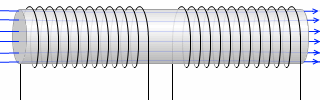さらには、磁場が漏れないように、鉄心をつなげてしまった方がいいです。

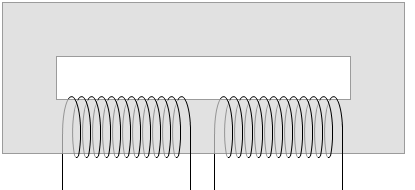その上さらに、鉄心の端からの磁場の漏れを無くすため、鉄心をぐるっと一周つなげた方がいいです。

相互インダクタンス

1次コイルの電流の大きさに応じて2次コイルにどのくらいの誘導起電力が発生するのか、考えてみます。

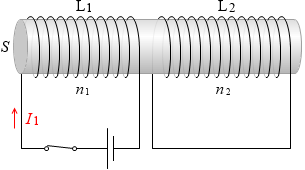1次コイルを L₁ 、2次コイルを L₂ とし、それぞれの単位長さ当たりの巻き数を n₁ [回/m] 、n₂ [回/m] 、2つのコイルの断面積を共に S [m²] 、2つのコイル内部の鉄心の透磁率を共に μ [N/A²] 、1次コイル L₁ に流れる電流を I₁ [A] とします。

コイル L₁ に I₁ の電流が流れるとき、コイル内部にできる磁場の磁束密度（=ソレノイドがつくる磁束密度）B₁ [Wb/m²] は、

　　　　B₁ = μn₁I₁

であり、磁束 Φ₁ [Wb] は、これに断面積 S を掛けたものだから、

　　　　Φ₁ = B₁S = μn₁I₁S

であり、どのくらい磁束が漏れてしまうか分かりませんが、コイル L₂ 内の磁束 Φ₂ [Wb] も

　　　　Φ₂ ∝ Φ₁

であることは予想されます。そして、コイル L₂ で発生する誘導起電力を V₂ [V] とすると、

　　　　V₂　∝　- n₂\(\large{\frac{ΔΦ_2}{Δt}}\)　　＊n₂ の n は小文字です。単位長さ当たりの巻き数です。
大文字の N であれば巻き数を表します。
あくまでも
　V₂　∝　- n₂\(\large{\frac{ΔΦ_2}{Δt}}\)
であって、
　V₂　=　- n₂\(\large{\frac{ΔΦ_2}{Δt}}\)
ではないことにご注意ください。
　閉じる

であるはずです。すなわち、

　　　　V₂　∝　- n₂\(\large{\frac{ΔΦ_2}{Δt}}\)　∝　- n₂\(\large{\frac{ΔΦ_1}{Δt}}\)　=　- n₂\(\large{\frac{Δ(μn_1 I_1 S)}{Δt}}\)　=　- μn₁n₂S\(\large{\frac{ΔI_1}{Δt}}\)

であるはずです。この μn₁n₂S の部分に比例する定数を M で表し、これを相互インダクタンスといいます＊ M は mutual inductance （相互のインダクタンス）から。

「μn₁n₂S の部分に比例する定数を M」 と分かりにくい表現をしてしまいましたが、M の中にはコイルの長さ l や下で説明する結合係数 k が含まれます。下で説明するように相互インダクタンスというものは普通は
　　M = \(\large{\frac{μN_1N_2S}{l}}\)
あるいは
　　M = μn₁n₂l₁S
とするものなのでこの式を覚えてしまってもいいですが、これは磁束漏れを考慮しておらず特別の場合にだけしか成り立たない式であるということを頭に入れておいてください。
　閉じる。単位は自己インダクタンスと同じく [H] ヘンリー です。

相互インダクタンスとは

V₂ = - M\(\large{\frac{ΔI_1}{Δt}}\) という式を見てみますと、コイル L₂ に発生する相互誘導による起電力 V₂ は相互インダクタンス M に比例しています。M が大きい方が相互誘導起電力が大きいということです。

そして、M ∝ μn₁n₂S でありますので、これを解釈しますと、透磁率の大きい物質が挿入されていて、双方のコイルの巻き密度が大きく、断面積が大きい方が、相互誘導起電力が大きくなる、といえます。

-（マイナス）はレンツの法則

V₂ = - M\(\large{\frac{ΔI_1}{Δt}}\) という式に -（マイナス）が付くのは、レンツの法則を表しているだけで、あまり強く意識する必要はありません。

コイルの巻き方の向きが変わってしまえば、起電力の向き、電流の向きも変わってしまいます。-（マイナス）が付くことを意識するより、レンツの法則、フレミングの左手の法則、あるいは右ねじの法則を間違わずに正確に適用することが大切です。

環状鉄心の相互インダクタンス

大学の教科書では、鉄心が環状の場合の相互インダクタンスについて取り上げられていることが多いと思いますが、環状鉄心コイルにおいては磁束が漏れないとみなすことができ、話が単純になります。簡単に説明しておきます。

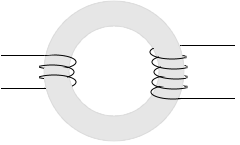1次コイル、2次コイルの巻き数を N₁、N₂ とし、鉄心の透磁率を μ、鉄心の中心部の円周の長さを l、鉄心の断面積を S、1次コイルに流れる電流を I₁ とします。

するとコイル内にできる磁場の磁束密度 B は

　　　　B = \(\large{\frac{μN_1 I_1}{l}}\)　　　（←大学の教科書を見てください）

であり、磁束 Φ は、これに断面積を掛けたものだから、

　　　　Φ = BS = \(\large{\frac{μN_1 I_1}{l}}\)S

であり、この磁束は2次コイルも貫くので＊上の『相互インダクタンス』のところの　Φ₂ ∝ Φ₁　が　Φ₂ = Φ₁　ということです。
　閉じる、2次コイルの誘導起電力 V₂ は

　　　　V₂ = - N₂\(\large{\frac{ΔΦ}{Δt}}\) = - N₂\(\large{\frac{μN_1SΔ I_1}{lΔt}}\) = - \(\large{\frac{μN_1N_2S}{l}}\)⋅\(\large{\frac{ΔI_1}{Δt}}\)

となります。定数の部分が相互インダクタンス M です。

　　　　M = \(\large{\frac{μN_1N_2S}{l}}\)

です。そして、1次コイルの自己インダクタンス L₁ は『自己誘導』項で説明したように、

　　　　L₁ = \(\large{\frac{μN_1^2S}{l}}\)

です。

次に逆に、2次コイルに電流 I₂ を流したとして、同じように自己インダクタンスと相互インダクタンスを求めてみますと、

　　　　M = \(\large{\frac{μN_1N_2S}{l}}\)

　　　　L₂ = \(\large{\frac{μN_2^2S}{l}}\)

となります。これら L₁ 、 L₂ 、M をよく見比べてみますと、

　　　　L₁×L₂ = M²

という関係があることが分かります。

理想的でないコイル間でも似たような関係があり、

　　　　M = k\(\sqrt{L_1L_2}\)

と表され、k のことを結合係数と呼びます。1次コイルから2次コイルへどのくらい漏れ無く磁束を伝えられるかを表していて、0 以上 1 以下の値をとります。（高校生は覚えなくていいです）