sin・cos
高校物理で頻出
高校物理ではあちこちで sin や cos というものが出てきます。これらを知ってないと高校物理はチンプンカンプンです。当サイトを読み始める前に必ず理解しておいてください。
三角比
sin(サイン)、cos(コサイン)というのは三角比の一種です。三角比というのは直角三角形における角や辺の大きさの関係を表す様々な法則のことです。
sin
 このような直角三角形において、
このような直角三角形において、
 \(\sinθ\) というのは青辺の長さと赤辺の長さの比のことです。\(θ\) の位置に注意してください。赤辺と離れた位置です。青辺と赤辺に挟まれた位置ではありません。
\(\sinθ\) というのは青辺の長さと赤辺の長さの比のことです。\(θ\) の位置に注意してください。赤辺と離れた位置です。青辺と赤辺に挟まれた位置ではありません。
\(\sinθ\) = 
たとえば、\(θ\)=30° のとき sin30° の値は \({\large\frac{1}{2}}\) であり、 = \({\large\frac{1}{2}}\) です。\(θ\)=30° のとき青辺は赤辺の2倍の長さです。
= \({\large\frac{1}{2}}\) です。\(θ\)=30° のとき青辺は赤辺の2倍の長さです。
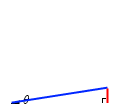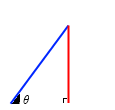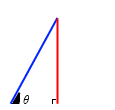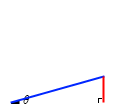 \(θ\) が大きくなると \(\sinθ\) =
\(θ\) が大きくなると \(\sinθ\) =  も大きくなります。
も大きくなります。
「sin」はカマキリの手をイメージしてください。クレーンとか。
 あるいは筆記体の「S」を描いて覚えてください。sin の「S」です。描き始めの小さい円は角の位置を表しています。重要です。この覚え方は直角三角形の形によっては「S」が描きにくいという欠点があります。
あるいは筆記体の「S」を描いて覚えてください。sin の「S」です。描き始めの小さい円は角の位置を表しています。重要です。この覚え方は直角三角形の形によっては「S」が描きにくいという欠点があります。
cos
 このような直角三角形において、
このような直角三角形において、
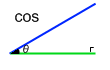 \(\cosθ\) というのは青辺の長さと緑辺の長さの比のことです。\(θ\) の位置に注意してください。青辺と緑辺に挟まれた位置です。
\(\cosθ\) というのは青辺の長さと緑辺の長さの比のことです。\(θ\) の位置に注意してください。青辺と緑辺に挟まれた位置です。
\(\cosθ\) = 
たとえば、\(θ\)=30° のとき cos30° の値は \({\large\frac{\sqrt{3}}{2}}\) であり、 = \({\large\frac{\sqrt{3}}{2}}\) ≒ \({\large\frac{1.73}{2}}\) です。
= \({\large\frac{\sqrt{3}}{2}}\) ≒ \({\large\frac{1.73}{2}}\) です。
 \(θ\) が大きくなると \(\cosθ\) =
\(θ\) が大きくなると \(\cosθ\) =  は小さくなります。
は小さくなります。
「cos」はコンパスをイメージしてください。トングとか。
 あるいは「C」の字を描いて覚えてください。cos の「C」です。
あるいは「C」の字を描いて覚えてください。cos の「C」です。
tan
tan(タンジェント)というのもあります。たまに出てきます。
 このような直角三角形において、
このような直角三角形において、
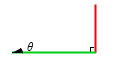 \(\tanθ\) というのは緑辺の長さと赤辺の長さの比のことです。\(θ\) の位置に注意してください。
\(\tanθ\) というのは緑辺の長さと赤辺の長さの比のことです。\(θ\) の位置に注意してください。
\(\tanθ\) = 
これは分母、分子を青辺の長さで割ると  となり、上の sin と cos の説明と見比べると \({\large\frac{\sinθ}{\cosθ}}\) であることがわかります。すなわち \(\tanθ = {\large\frac{\sinθ}{\cosθ}}\) です。
となり、上の sin と cos の説明と見比べると \({\large\frac{\sinθ}{\cosθ}}\) であることがわかります。すなわち \(\tanθ = {\large\frac{\sinθ}{\cosθ}}\) です。
 「t」の字を描いて覚えてください。tan の「t」です。
「t」の字を描いて覚えてください。tan の「t」です。
90°-\(θ\)
直角三角形の一つの角が \(θ\) である場合、もう一方の角が 90°-\(θ\) になることはご存知でしょうか。三角形の3つの角の合計は必ず 180° です。直角三角形は1つの角が 90° であるわけですから、残り2つの角の合計は 90° です。というわけで、もう一方の角は 90°-\(θ\) になります。このことにより sin と cos には以下のような関係があります。
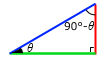 このような直角三角形において、
このような直角三角形において、
\(\sinθ\) =  = cos(90°-\(θ\)) つまり \(\sinθ\) = cos(90°-\(θ\))
= cos(90°-\(θ\)) つまり \(\sinθ\) = cos(90°-\(θ\))
\(\cosθ\) =  = sin(90°-\(θ\)) つまり \(\cosθ\) = sin(90°-\(θ\))
= sin(90°-\(θ\)) つまり \(\cosθ\) = sin(90°-\(θ\))
具体的な数値
sin23° 、cos40° などの具体的な数値は三角関数表を見て調べます。数学の教科書の巻末に載ってます。あるいは高機能電卓に打ち込んで調べます。sin23° ≒ 0.3907 、cos40° ≒ 0.7660 です。
以下の直角三角形に関しては数値を暗記しなければなりません。
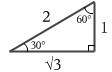 sin30° = \({\large\frac{1}{2}}\) 、sin60° = \({\large\frac{\sqrt{3}}{2}}\) 、cos30° = \({\large\frac{\sqrt{3}}{2}}\) 、cos60° = \({\large\frac{1}{2}}\) です。
sin30° = \({\large\frac{1}{2}}\) 、sin60° = \({\large\frac{\sqrt{3}}{2}}\) 、cos30° = \({\large\frac{\sqrt{3}}{2}}\) 、cos60° = \({\large\frac{1}{2}}\) です。
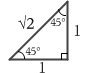 sin45° = \({\large\frac{1}{\sqrt{2}}}\) 、cos45° = \({\large\frac{1}{\sqrt{2}}}\) 、tan45° = 1 です。
sin45° = \({\large\frac{1}{\sqrt{2}}}\) 、cos45° = \({\large\frac{1}{\sqrt{2}}}\) 、tan45° = 1 です。
あと、辺の比が 3:4:5 の直角三角形があることも覚えておいた方がいいかもしれません。これは角度は覚える必要はありません。
あと、
 sin0° = 0
sin0° = 0  cos0° = 1
cos0° = 1
 sin90° = 1
sin90° = 1  cos90° = 0
cos90° = 0
も頭に入れておいてください。
実際には高校物理では具体的な数値を答えさせるような問題は少なく、大抵の場合、変数 \(θ\) を用いて \(mg\cosθ\) とか \(l\sinθ\) などと解答します。
なぜ「直角」三角形なのか
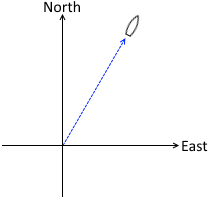 真北から東へ30°傾いた向きへ船が時速30kmで進んでいるとします。
真北から東へ30°傾いた向きへ船が時速30kmで進んでいるとします。
このときの東向きの速度の成分を考えるとき、
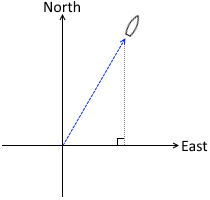 東西軸に垂線を下ろすことになります。
東西軸に垂線を下ろすことになります。
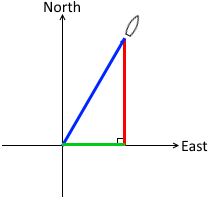 すると直角三角形ができます。
すると直角三角形ができます。
ある方向の成分を考える → 垂線を下ろす → 直角三角形ができる 、ということです。
上の例では、速度の東向きの成分は 30[km/h] × cos60° = 30[km/h] × \({\large\frac{1}{2}}\) = 15[km/h] です。
例
 sin と cos はどっちがどっちなのかとても間違いやすいです。慣れが必要です。
sin と cos はどっちがどっちなのかとても間違いやすいです。慣れが必要です。
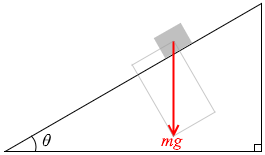
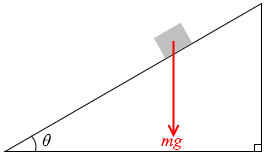 たとえば斜面に置かれた物体に掛かる重力を
たとえば斜面に置かれた物体に掛かる重力を
(慣れないうちは長方形の補助線を描いてください)
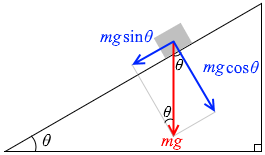 運動方向の成分が \(mg\sinθ\) で、それに垂直な方向の成分が \(mg\cosθ\) です。
運動方向の成分が \(mg\sinθ\) で、それに垂直な方向の成分が \(mg\cosθ\) です。
(\(θ\) については『斜面上の運動』参照)
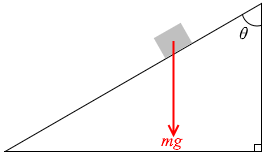 あまり無いことですが
力のモーメントを考えるときにはしばしばあります。
、
あまり無いことですが
力のモーメントを考えるときにはしばしばあります。
、
\(θ\) が左図のような角に設定されている場合は
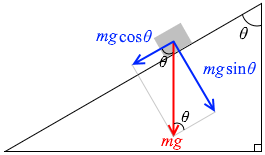 sin と cos は入れ替わります。
sin と cos は入れ替わります。
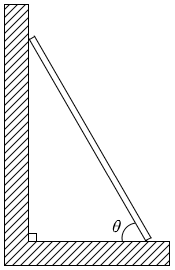 他に sin、cos がよく登場するのが、剛体のつり合いの問題です。
他に sin、cos がよく登場するのが、剛体のつり合いの問題です。
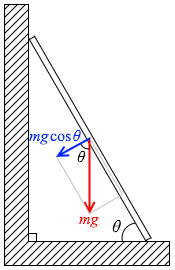 棒に掛かる重力の、棒に垂直な方向の成分は \(mg\cosθ\) で、
棒に掛かる重力の、棒に垂直な方向の成分は \(mg\cosθ\) で、
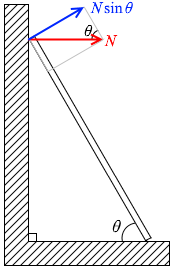 壁からの垂直抗力の、棒に垂直な方向の成分は \(N\sinθ\) です。
壁からの垂直抗力の、棒に垂直な方向の成分は \(N\sinθ\) です。
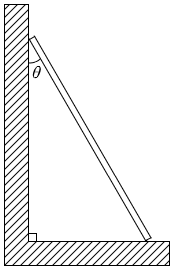 これも \(θ\) の設定が変われば sin と cos が入れ替わります。
これも \(θ\) の設定が変われば sin と cos が入れ替わります。
あとコツとして、自分で三角形を作図するときは、直角二等辺三角形 のような三角形でなく、細長い三角形
のような三角形でなく、細長い三角形 を描いた方がいいです。
を描いた方がいいです。
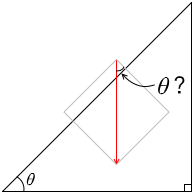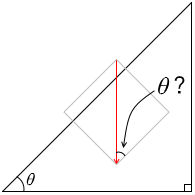 直角二等辺三角形のような三角形を描いてしまうと \(θ\) の位置がわからなくなりがちです。
直角二等辺三角形のような三角形を描いてしまうと \(θ\) の位置がわからなくなりがちです。