有効数字
測定値
\(π\) というのは 3.141592… という数値のことであり、\(\large\frac{\sqrt{3}}{2}\) というのは 0.8660254… という数値のことでありますが、これらは理論的に求められた値です。 物理定数に関しては定義されたものと測定されたものと2種類ありますが、測定されたものの方も桁数がとても多いので理論値であるかのように扱います。特別な精密さが求められるとき以外は物理定数は測定値ではなく理論値である、とみなします。
一方、12.3mm、43.2g などと示された場合のこれらの値は、測定器によって測られたものです。測定値です。
そして、測定値は真の値ではありません。真の値はたとえば 12.34567898mm、43.21012345g というものだったりします。
このとき、もっと精度の高い測定器で測れば 12.34mm、43.21g といった値を得られるだろうし、精度の低い測定器で測れば 12mm、43g という値しか得られなかったりします。
このように測定値というのは近似値であり、真の値とは誤差があります。 精度の高さについては決まりがあるわけではなく、目的によって変わります。車が車庫に入るかどうかを知りたいときにミリ単位まで計測する必要はないでしょうが、車のエンジンのピストンを作るときにはミリ単位より細かい単位まで計測する必要があります。
有効数字とは
ある物体の質量について真の値が 43.21012345g であったりした場合、小数第2位まで正確に測れる測定器では測定値は 43.21g となりますが、このときの 4、3、2、1 という数字を有効数字といいます。小数第3位まで正確に測れる測定器であれば測定値は 43.210g となり、有効数字は 4、3、2、1、0 となります。
測定値と真の値の関係
測定値が 43.2g であると示されたとき、それは小数第2位を四捨五入して 43.2 という値を得ているわけですが、このときの真の値は、
43.15g かもしれないし、
43.1985972g かもしれないし、
43.2000000000001g かもしれないし、
43.213723558g かもしれないし、
43.2499999999g かもしれません。
43.2g と示されたとき、真の値（\(x\) と置く）は、
43.15 ≦ \(x\) ＜ 43.25
の範囲の中にあります。
これが有効数字の意味するところです。
有効数字の桁数
有効数字で問題となるのはその桁数（有効桁数）です。たとえば次のような数値の有効数字の桁数はおわかりでしょうか。
0.043 有効数字2桁です
0.0432 有効数字3桁です
0.00432 有効数字3桁です
0.000432 有効数字3桁です。左側の0は無関係です。
0.0430 有効数字3桁です
0.04300 有効数字4桁です
0.0430000 有効数字6桁です。右側の0は意味があります。わざわざ付け足された0です。
4.3 有効数字2桁です
4.32 有効数字3桁です
4.321 有効数字4桁です
43.21 有効数字4桁です
43.20 有効数字4桁です
432.00 有効数字5桁です
432.000 有効数字6桁です
4.32×102 有効数字3桁です
4.32×103 有効数字3桁です
4.321×103 有効数字4桁です
43.21×102 有効数字4桁です
432 有効数字3桁です
4320 有効数字不明です。位取りの0なのか有効数字の0なのか判別できません。
432000 有効数字不明です
432000 は有効数字3桁かもしれないし、4桁、5桁、6桁かもしれません。はっきりさせるには
4.32 × 105 （有効数字3桁）とか …①
43.2 × 104 （有効数字3桁）とか
4.320 × 105 （有効数字4桁）とか …②
43.20 × 104 （有効数字4桁）と指数表記法（科学的表記法）で書かなければいけません。
普通は①、②のように小数点より大きい桁は1桁（0を除く1~9）にします。他の数値と見比べやすくしたいときはそうしない場合もあります。
有効数字の計算
1.2mm という値が示されたとき、真の値は 1.15 ≦ \(x\) ＜ 1.25 の範囲にあるわけですが、これはつまり1の位はゆるぎがなく確かで、小数第1位の位はやや不確かで、小数第2位の位は不明、ということです。
12.34mm という値が示された場合であれば、小数第1位以上がゆるぎがなく確かで、小数第2位がやや不確かで、小数第3位が不明、ということになります。
有効数字というのは末位の数がやや不確かになっています。
加算・減算では有効数字の末位が高い方に合わせる
2.34mm に 5.6mm を単純に足すと 7.94mm になりますが、この数値は測定値を足し合わせたものとしては不適切です。
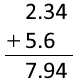7.94 の 9 は 3 とやや不確かな 6 を足したものなのでやや不確かです。さらに、7.94 の 4 は 4 と 0 を足したものではなく、4 と不明な何かを足したものです。この 4 は数値として意味をなしません。明記することは不適切です。
とういことで、2.34mm に 5.6mm を足したものは 7.9mm とするのが適切です。
有効数字の加算・減算では、その答えは有効数字の末位の高い方の位に合わせます。
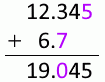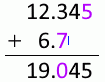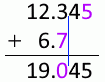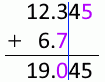12.345mm 足す 6.7mm は 19.0mm です。
123.45mm 足す 6.7mm は 130.2mm です。
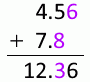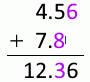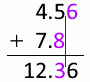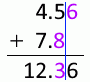4.56mm 足す 7.8mm は 12.4mm です。小数第1位までとなるようにされてることに変わりありませんが、有効桁数が（7.8mmの2桁から12.4mmの3桁に）増えてます。加算においては有効桁数が1桁増えることが起こりえます。
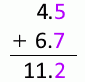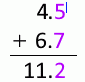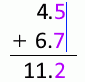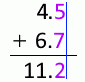4.5mm 足す 6.7mm は 11.2mm です。やや不確かな 5 とやや不確かな 7 を足した 2 はちょっと不確か、とでもいえますがいちおう有効数字とします
4.5mm の真の値を \(x\) 、6.7mm の真の値を \(y\) とすると
4.45 ≦ \(x\) ＜ 4.55 、6.65 ≦ \(y\) ＜ 6.75
∴ 4.45 + 6.65 ≦ \(x\) + \(y\) ＜ 4.55 + 6.75
∴ 11.10 ≦ \(x\) + \(y\) ＜ 11.30
ですがこれは 11.2mm と示された場合の真の値（\(z\) と置く）の範囲
11.15 ≦ \(z\) ＜ 11.25
と矛盾します。
。たくさん足し合わせた場合、たとえば 2.3mm と 3.4mm と 4.5mm と 5.6mm を足し合わせた場合 15.8mm とするのがいちおうの正解ですが、小数第1位の 8 はかなり不確かな数値です。
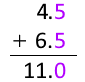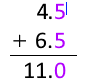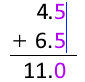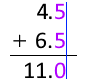似た問題としてうっかりしがちなのが、4.5mm 足す 6.5mm を 11mm としてしまうことです。高校理科として正しいのは 11.0mm です。
減算についても考えてみます。
123.4mm 引く 5.678mm は 117.7mm です。
12.001mm 引く 12.0001mm は 0.0009mm です。有効数字の桁数も末位の位置も変わってしまっています。このような計算は高校理科では出てきませんが頭の隅に入れておいてください。
差が小さい数値同士の減算のときにだけ出てくる現象です。桁落ちといいます。コンピューターを使った計算ではこの問題に対して独特の方法で対処します。
乗算・除算では有効桁数が少ない方に合わせる
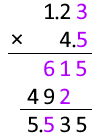1.23mm と 4.5mm を掛け合わせた数値について考えてみます。
1.23 と 4.5 を単純に掛け合わせると 5.535 になりますが、計算途中でやや不確かな 6 が現れます。この 6 は 5.535 の上から2番目の位に影響を与えます。有効な位はここまでとすべきです。それより小さい位はだいぶ不確かなので四捨五入すべきです。
615 の 1 について考えてみますと、これはやや不確かな 3 とやや不確かな 5 を掛け合わせたものから来ています。 上の説明では、やや不確かなものとやや不確かなものを足し合わせたらちょっと不確か、としましたが、掛け合わせた場合はそれよりもさらに不確かです。その 1 の下にある 2 はやや不確かな 3 と 4 を掛け合わせたもので、不確かさを4倍にしています。
というわけで小数第2位を数値に含めることは不適切です。
小数第3位はいわずもがなで、もっと不適切です。
1.23mm 掛ける 4.5mm は 5.5mm2 とするのが適切です。
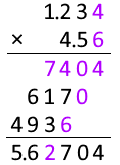同じように、
1.234mm 掛ける 4.56mm は 5.63mm2 です。
1.2345mm 掛ける 4.567mm は 5.638mm2 です。
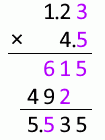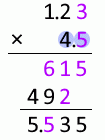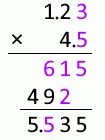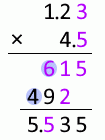
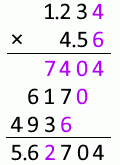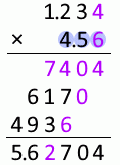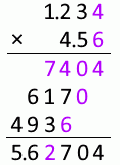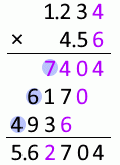
結局、有効桁数の少ない方の桁数と、計算結果の上から何桁目にやや不確かな数が現れるかが一致します
といいたいところですが完全には一致しません。繰り上げが影響する場合があります。
3.000mm 掛ける 3.04mm では、やや不確かな数が上から3桁目に出てきてほしいところですが2桁目に出てきます。
このような場合でも3桁にして 9.12mm2 とします。
3.000mm 掛ける 4.03mm では、やや不確かな数が上から3桁目に出てきてほしいところですが4桁目に出てきます。
このような場合でも3桁にして 12.1mm2 とします。
。
また、計算機を用いて計算するときは数字をそのまま入力すればいいのですが、筆算をするときは桁数が多い方を短くして計算を楽にします。少ない方の桁より1桁多い桁まで減らします。
たとえば、1.2345mm に 4.5mm を掛けるときは 1.2345 の上から4桁目を四捨五入
このとき四捨五入ではなく切り捨てをする流儀もあるようですが、それはおそらく計算結果が真の値より小さくあってほしいという事情があるのだと思います。
ビールの瓶を作る担当者にとっては計算結果が真の値より小さい方が確実だし、ビールの中身を作る担当者にとっては計算結果が真の値より大きい方が確実です。逆だとビールが瓶からあふれてしまう恐れがあります。
して3桁（1.23mm）にしてから計算します。別に5桁目を四捨五入して4桁（1.235mm）にするのでも構いません。多い分には構いません。計算し終わってからちゃんと2桁にすればO.K.です。
ちなみに四捨五入というのは同じ数字に対して2回行っていけません。
1.149 の小数第3位を四捨五入して 1.15 としてから小数第2位を四捨五入して 1.2 とするようなことしてはいけません。1.149 からだいぶ離れてしまいます。
このやり方は \(π\) や 桁数の多い物理定数を含む計算のときでも同じです。
次に説明する除算においても同じです。
4.321mm2 割る 1.23mm を考えてみます。
123 を3倍した 369 の 9 はやや不確かで、これはその下の方にある 160 の先頭の 1 を生み出しているので 160 という数字はやや不確かであり、これにあてがう 123 × 1 もやや不確か、ということになります。
つまり、3.513… の 1 のところまでを有効数字とするのが適切です。
逆に、1.23mm2 割る 4.321mm を考えてみます。
1.23 の 3 はやや不確かであり、これはその下の方にある 20120 の先頭の 2 を生み出しているので 20120 という数字はやや不確かであり、これにあてがう 4.321 × 4 もやや不確か、ということになります。
つまり、0.2846… の 4 のところまでを有効数字とするのが適切です。
というわけで乗算と同じように、有効桁数の少ない方の桁数と、計算結果の上から何桁目にやや不確かな数が現れるかが一致します
といいたいところですが乗算と同じように除算でも完全には一致しません。
たとえば 4.321mm2 割る 7.65mm では、やや不確かな数が上から3桁目に出てきてほしいところですが4桁目に出てきます。
このような場合でも3桁にして 0.565mm とします。
。
有効数字の乗算・除算では、その答えは有効桁数が少ない方に合わせます。