ばね振り子の力学的エネルギー_補足
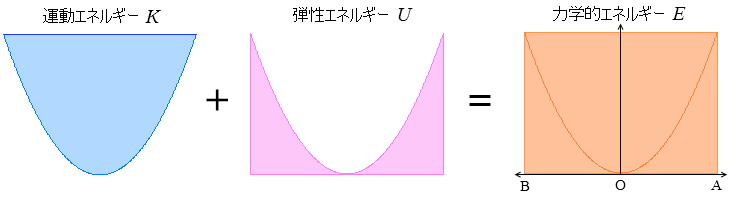
ばね振り子における K + U = E のイメージ
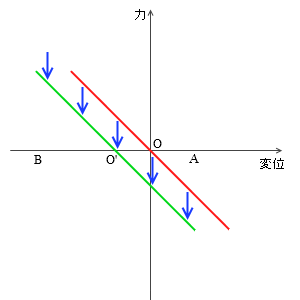
ばね振り子における正負
水平ばね振り子におけるX点でのおもりの速さを求める計算において、
vx2 = \(\large{\frac{k}{m}}\)(a2 - x2)
∴ vx = \(\sqrt{\frac{k}{m}(a^2-x^2)}\)
としてしまいましたが、これは、「速さ」といったらスカラー(正の値しかとらない)であるため ± を付けませんでした。仮に「速度」を求めるとなるとこれはベクトル(正負の値をとる)なので、
vx2 = \(\large{\frac{k}{m}}\)(a2 - x2)
∴ vx = ± \(\sqrt{\frac{k}{m}(a^2-x^2)}\)
とするべきです。
そしてこれは、正の値のときが右向きで、負の値のときが左向きであることを示しています。X点におけるおもりは、右向きに動いている瞬間と左向きに動いている瞬間の2通りあります。
また \(\sqrt{\ \ \ }\) の中身についてですが、k も a も m も定数であり、正であります。そして題意から、x ≦ a であるので、\(\sqrt{\ \ \ }\) の中身 \(\frac{k}{m}(a^2-x^2)\) は正です。
また、鉛直ばね振り子におけるO点でのおもりの速さを
vO = \(\sqrt{-gd + \large{\frac{ka^2}{m}}}\)
と説明しましたが、この \(\sqrt{\ \ \ }\) の中身は負になってしまうことがありえます。
vO = \(\sqrt{-gd + \large{\frac{ka^2}{m}}}\) mg = kd を代入して
= \(\sqrt{-gd + \large{\frac{ga^2}{d}}}\)
= \(\sqrt{gd(-1 + \large{\frac{a^2}{d^2})}}\)
a < d のとき \(\sqrt{\ \ \ }\) の中身が負になってしまいます。
しかし、a < d というのは、ばねの振幅が d より小さいときという意味です。A点がO点より下にあるということです。このときはおもりはO点を通りません。O点より低い位置で往復運動をしているということです。つまり、a < d の場合は、O点でのおもりの速さは定義されていない、存在しない、ということになります。
このように厳密な話をするとキリがないのですが、ばね振り子はどっちみち、中心からの距離が大事で、どっちを向いて運動しているかは関係ないので、あまり正負にこだわらずに議論を進めていったりします。
鉛直ばね振り子における中心について
本編で、鉛直のばね振り子は、自然長を中心としてではなく、つり合いの位置を中心とした水平のばね振り子、とみなすことができる、と説明しましたが、そのことをもう少し詳しく説明します。
| 弾性力 | 弾性力+重力 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A点(最上端) | - k(a - d) | - k(a - d) - mg = - k(a - d) - kd = - ka | |||||||
| X点(任意の位置) | - k(y - d) | - k(y - d) - mg = - k(y - d) - kd = - ky | |||||||
| O点(自然長) | 0 | 0 - mg = - kd | |||||||
| O'点(つり合いの位置) | - k(- d) = kd | kd - mg = kd - kd = 0 | |||||||
| B点(最下端) | - k(- a - d) = k(a + d) | k(a + d) - mg = k(a + d) - kd = ka |
この表を読み解くと、「弾性力+重力」というものを考えれば、O'点を中心とした水平ばね振り子とみなせることがわかります。O'点を中心にして変位と力が - k を比例定数として比例関係にあるからです。このことは、『ばね振り子』項の『自然長の位置を原点にとると』でも説明しました。
このことをイラストで説明すると以下のようになります。
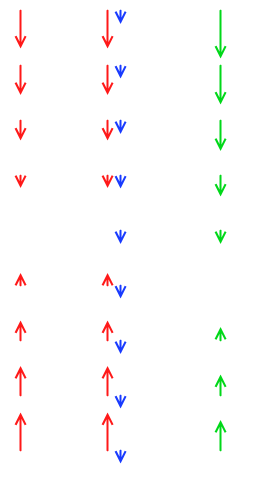 ↓ 弾性力
↓ 弾性力
↓ 重力
↓ 弾性力+重力
赤矢印の長さと青矢印の長さを足すと緑矢印の長さになります。
左側の赤矢印の列は、右側の緑矢印の列と実質的に同じものです。中心の位置が変わっただけのものです。
さらにグラフで説明すると以下のようになります。