図3のように、なめらかで質量の無視できる滑車を天井に固定して糸をかけ、糸の両端に質量 m の物体Aと質量 3m の物体Bを取り付ける。糸がたるまない状態で、Aが床に接するように、Bを手で支えた。このとき、Bの床からの高さは h であった。手を静かに離すと、Bは下降してやがて床に到達し た。Bが動き出してから床に達するまでの時間 t を式で表わせ。ただし、重力加速度の大きさを g とする。
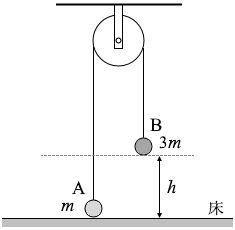
#センター12本試
図3のように、なめらかで質量の無視できる滑車を天井に固定して糸をかけ、糸の両端に質量 m の物体Aと質量 3m の物体Bを取り付ける。糸がたるまない状態で、Aが床に接するように、Bを手で支えた。このとき、Bの床からの高さは h であった。手を静かに離すと、Bは下降してやがて床に到達し た。Bが動き出してから床に達するまでの時間 t を式で表わせ。ただし、重力加速度の大きさを g とする。

#センター12本試
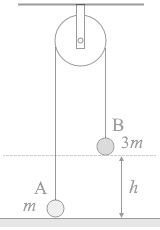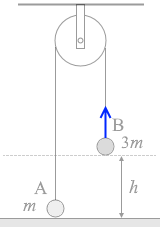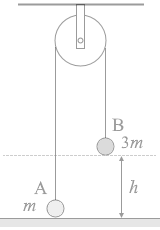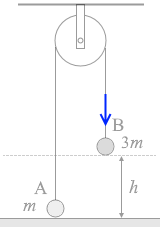 ピンと張った糸においては張力はどこもかしこも一定です。T と置きます。
ピンと張った糸においては張力はどこもかしこも一定です。T と置きます。
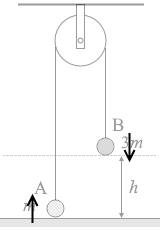 糸が伸びたり縮んだりしなければ、物体Aと物体Bは一緒に動き、速さ、加速度の大きさが同じです。加速度の大きさを a と置きます。
糸が伸びたり縮んだりしなければ、物体Aと物体Bは一緒に動き、速さ、加速度の大きさが同じです。加速度の大きさを a と置きます。
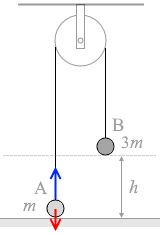 物体Aについての運動方程式を立てますと、
物体Aについての運動方程式を立てますと、
ma = T - mg ……➊
(問題文に「Aが床に接するように」とありますが、「糸がたるまない状態で」ともありますので、これはAと床の間に力ははたらいていないということです。0.001mm 隙間があいているとみなしてもいいです。)
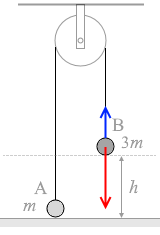 物体Bについての運動方程式を立てますと、
物体Bについての運動方程式を立てますと、
3ma = 3mg - T ……➋
(正負を物体Aの場合と合わせると、)
( - 3ma = - 3mg + T )
(と立式することもできます。同じことですが。)
➊式、➋式の両辺を足し合わせて T を消去すると、
ma + 3ma = - mg + 3mg
∴ 4ma = 2mg
∴ a = \(\large{\frac{1}{2}}\)g
物体Aと物体Bはこの加速度で運動します。
等加速度直線運動の式 x = v0t + \(\large{\frac{1}{2}}\)at2 を立てますと、
h = 0 + \(\large{\frac{1}{2}}\)⋅\(\large{\frac{1}{2}}\)gt2
∴ \(\large{\frac{4h}{g}}\) = t2
∴ t = \(\sqrt{\large{\frac{4h}{g}}}\)
(余談:1)
a の値を➊式に代入して張力 T を求めてみますと、
\(\large{\frac{1}{2}}\)mg = T - mg
∴ T = \(\large{\frac{3}{2}}\)mg
物体Aの重力より大きく、物体Bの重力より小さくなっています。
(余談:2)
本問は『糸でつながれた物体』項の
M → m 、m → 3m
の場合に相当します。(本問では滑車は右回り)