波動

波動とは

ロープの一端を柱に固定し、もう一端を手で上下に振動させると、波が柱に向かっていきます。しかしこのときロープは上下に振動をしているだけで、壁の方向へ移動しているわけではありません。

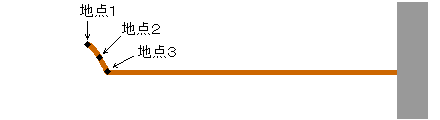地点1は地点2を引っ張り上げ、地点2は地点３を引っ張り上げ、…という風に次々と振動が伝わっていきます。このような動きを波動、または波といいます。地点1が地点2に影響を及ぼさないと波は起こりません。たとえば砂場では波は起こりません。砂粒は隣の砂粒を引っ張り上げないからです。水面に波が起こるのは水分子が隣の水分子を分子間力によって引っ張り上げるからです。

最初に振動を始めた手の位置を波源といい、波を伝える物質（ロープ）を媒質といいます。水面上の波の媒質は水です。音の媒質は空気です。

手を一度しか振動させないと波は1つしか起こらず、このような単発の波をパルス波（孤立波）といいます。（単発波ではなく角張った波形の波のことをパルス波ということもあります）。手を何度も上下してできた波を連続波といいます。

波の要素の名称

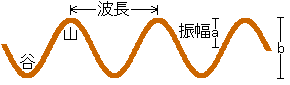波のくり返し1つ分の長さを波長といいます。量記号に \(λ\) を用います＊ なぜ \(λ\) を使うのかはわかりません 閉じる 。

波の高さ（左図の\(a\)）を振幅といいます。（\(b\)ではないので気をつけてください）。量記号に主に \(A\) を用います＊ Amplitude（振幅）から 閉じる 。

媒質が1秒間に往復する回数を振動数（または周波数）といい、量記号に \(f\) を用います＊ frequency（頻度）から 閉じる 。単位は [Hz] ヘルツ です＊ 19世紀のドイツの物理学者 ハインリヒ・ヘルツ から 閉じる 。[Hz] = [1/s] です。1秒間に4往復したら周波数は 4Hz です。1秒間に4つの波を送り出すという意味です。

1往復に要する時間を周期といい、量記号に主に \(T\) を用います＊ おそらく time から。でも、周期を英訳すると cycle または period。。。 閉じる 。1秒間に4往復したときは、1往復に0.25秒かかるので周期は 0.25s です。（『周期と回転数』参照）

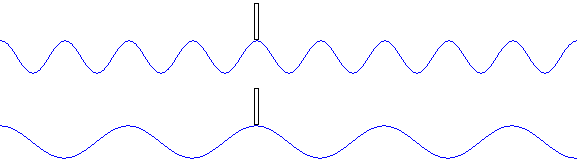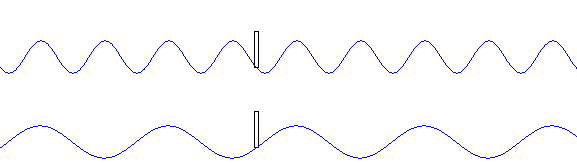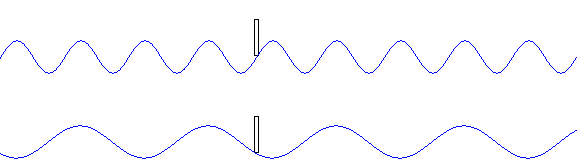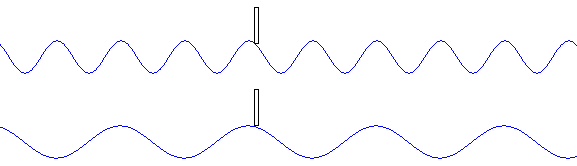
右の振動は左の振動に比べて、
振動数が高い（=振動数が大きい=周波数が高い=周波数が大きい=周期が短い=周期が小さい）です。

波の基本式

振動数 \(f\) [Hz] は周期 \(T\) [s] の逆数なのでその関係は以下のようになります。

エフ イコール ティーブンノイチ　です。

波が進む速さ（1秒間に進む距離）\(v\) [m/s] は、振動数（1秒間に送り出す波の数）\(f\) [1/s] と波長（1つの波の長さ）\(λ\) [m] を掛け合わせたものです。

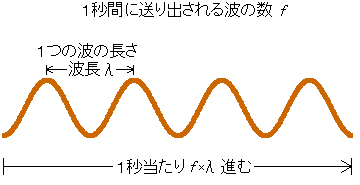波長 \(λ\) が一定の場合は、振動数 \(f\) が大きくなるほど速さ \(v\) が大きくなり、
振動数 \(f\) が一定の場合は、波長 \(λ\) が大きくなるほど速さ \(v\) が大きくなり、
速さ \(v\) が一定の場合は、振動数 \(f\) が大きくなるほど波長 \(λ\) が小さくなります。

つまり以下のようになります。

ヴイ イコール エフラムダ　です。＊ この式に上の　\(f = \large{\frac{1}{T}}\)　を代入すれば　\(v = \large{\frac{λ}{T}}\)　です 閉じる

この式は基本中の基本です。絶対に覚えましょう。

●波長 \(λ\) が同じとき、振動数 \(f\) が大きいほど、波の速さ \(v\) が大きくなる。

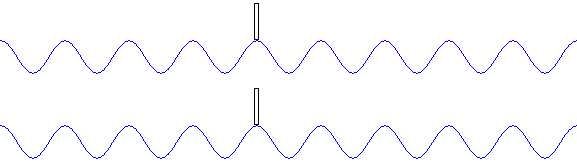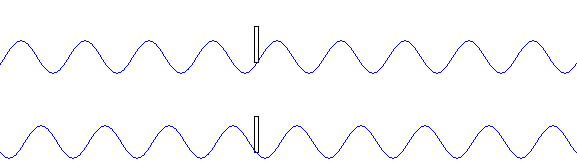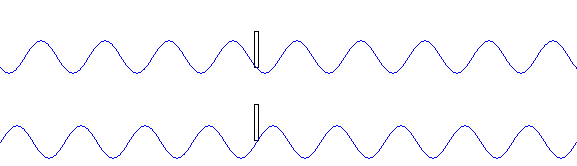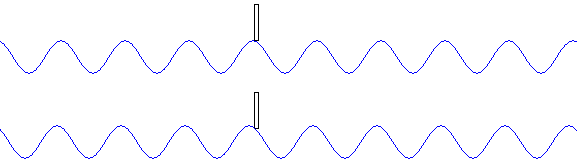
●振動数 \(f\) が同じとき、波長 \(λ\) が大きいほど、波の速さ \(v\) が大きくなる。

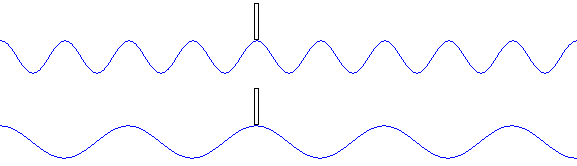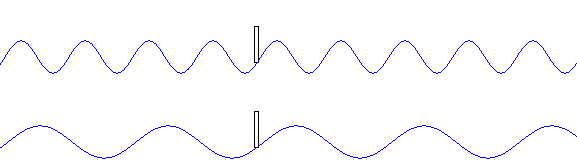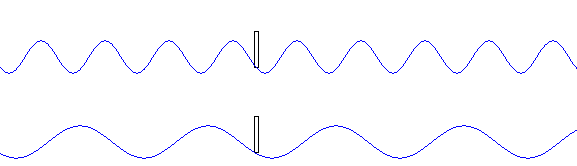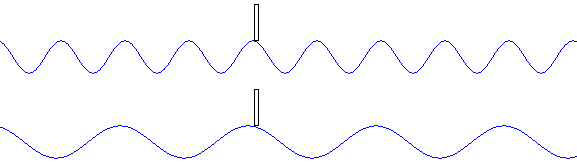
●波の速さ \(v\) が同じとき、振動数 \(f\) が小さいほど、波長 \(λ\) が大きくなる。