円運動

等速円運動

物体が円周上を一定の速さで運動するとき、この運動を等速円運動といいます。単振動や波動を考えるときの大本となる運動です。

角速度

基準となる原点から運動している物体に引いたベクトルを動径ベクトルといいますが、等速円運動においては円の中心から物体に引いたベクトルが動径ベクトルとなります。

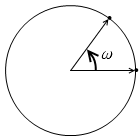円運動において動径ベクトルが1秒間に回転する角度を角速度といいます。回転の速さを表す量です。

単位はラジアン毎秒 [rad/s] で、量記号は ω を用います。

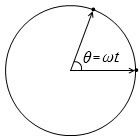
t [s]秒間に θ [rad] だけ回転したときの角速度 ω [rad/s] は、以下のように表せます。

（『位相』項もご参照ください。）

等速円運動の速さ

半径 r [m] の円周上を等速円運動する物体の動径ベクトルが t [s]秒間に θ [rad] だけ回転したとき、物体が進んだ距離 l [m] は、

となります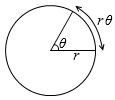＊ 半径 r の円において中心角 1rad の円弧の長さが r なのだから
半径 r の円において中心角 0.8rad の円弧の長さは 0.8r
半径 r の円において中心角 1.2rad の円弧の長さは 1.2r
半径 r の円において中心角 θrad の円弧の長さは θ r
　閉じる。これを時間 t で割って、周回する物体の速さ v [m/s] を求めると、

　　　　v = \(\large{\frac{l}{t}}\) = \(\large{\frac{r\theta}{t}}\)

となり、これに上で示した ω = \(\large{\frac{\theta}{t}}\) を代入すると、

となります。『向心力』項のまとめも参照してください。

周期と回転数

物体が等速円運動するとき、1周するのに要する時間 T [s] を周期といいます（『波の要素の名称』参照）。1周の長さは 2πr [m] であり、周回する速さは v = rω [m/s] であり、（時間）=（長さ）÷（速さ）なので、

　　　　T = \(\large{\frac{2\pi r}{r\omega}}\) = \(\large{\frac{2\pi}{\omega}}\)　＊これは、1周分の角度 2π を1秒間当たりの角度（つまり角速度） ω で割ったものと考えてもいいです。
　閉じる

となります。

また、物体が1秒間に回転する回数を回転数といい（波動においては振動数あるいは周波数）、量記号は n で表し＊おそらく number of times から。
n でなく f を用いることもあります。
　閉じる、単位に [Hz] ヘルツ を用います＊[Hz] を [回/s] と表現することもあります。
　閉じる。

回転数 n は周期 T の逆数だから＊ 1周に0.2秒かかるなら、1秒間に5回転する。
1周に0.4秒かかるなら、1秒間に2.5回転する。
1周に2秒かかるなら、1秒間に0.5回転する。
1周に4秒かかるなら、1秒間に0.25回転する。
　閉じる

となり、変形しますと ω = 2πn とも表現できます。2π というのは単なる定数（数値でいうとだいたい 2×3.14=6.28）ですので、ω と n はほぼ同じ性質の量ということが分かります。