くさび形空気層による光の干渉
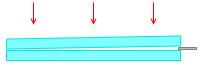2つの平面ガラスの一方の端に薄い紙などを挟むと、その間にくさび形の空気層ができます。このときガラスの上から垂直に単色光を当て、上から覗き見ると、縞模様が現れます。このときの縞の間隔を探ってみます。
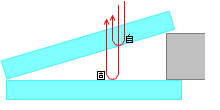左図は上下方向に大げさに拡大した図です。上のガラスの下面では、自由端反射となり位相はズレません。下のガラスの上面では、固定端反射となり位相が \(π\) ズレます。
今回の場合、上のガラスの上面での反射光と下面での反射光との干渉は考えません。薄膜による干渉（垂直に当たる場合）は、上から見たときに全体的に明るく見えるか暗く見えるか、という話でしたが、今は、上から見たときに局所的に干渉縞がどのように見えるか、という話です。
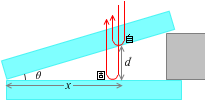左図のように符号を割り振りますと、2つの波の光路差は \(2d\) で、下まで進んでいった波は固定端反射して位相が \(π\) ズレるので、光路差が \((m+{\large\frac{1}{2}})λ\) のときに波が強め合います。（ 薄膜による干渉（垂直に当たる場合） と同じです）。つまり \(2d = (m+{\large\frac{1}{2}})λ\) となる場所に明線ができます。暗線ができるのは \(2d = mλ\) となる場所です。
さらに、\(d = x\tanθ\) であるので、干渉条件は以下のようになります。
くさび形空気層
明るくなる条件 \(\boldsymbol{2x\tanθ = (m + {\large\frac{1}{2}})λ}\)
暗くなる条件 \(\boldsymbol{2x\tanθ = mλ}\)
\((m = 0,1,2,…)\)
また、この式より、明線ができる位置 \(x\) は
\(2x\tanθ = (m + {\large\frac{1}{2}})λ\)
\(x = {\large\frac{(m+\frac{1}{2})λ}{2\tanθ}}\)
明線と明線の間隔 \(Δx\) は
\(Δx = x_{m+1} - x_m\)
\(= {\large\frac{(m+1+\frac{1}{2})λ}{2\tanθ}} - {\large\frac{(m+\frac{1}{2})λ}{2\tanθ}}\)
\(= {\large\frac{λ}{2\tanθ}}\)
となります。
\(\tanθ\) が分母にあるということは、ガラスに挟みこむ物の高さが小さいほど、明線と明線の間隔（縞模様の間隔）\(Δx\) が大きくなるということです。この式を使うことにより、干渉縞の間隔から照射光の波長を求めたり、2つのガラス板の角度などが特定できます。
また、くさび形空気層の場合の \(m\) という数字ですが、これは、線が何番目であるかを表しています。ガラス板とガラス板が接触する交線（\(d = 0\) となる位置。左図でいうと一番左側）から数えて何番目かということです。左図では、縞模様の明線が59本描かれてますが、一番左の線が \(m = 0\) のときの線で、一番右の59番目の線が \(m = 58\) のときの線です。