ニュートンリング
平面ガラスの上に大きな曲率半径の平凸レンズ（片面が平ら、片面が球面）を載せて、上から単色光を当て、上から覗き見ると、同心円の明暗の縞が見えます。
この縞をニュートンリングといいます。あの有名なニュートンが発見しました。
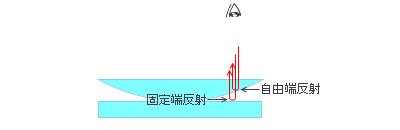原理はくさび形空気層の干渉とまったく同じです。
上の平凸レンズの下面での反射は自由端反射となり、位相はズレません。下の平面ガラスの上面での反射は固定端反射となり、位相が \(π\) ズレます。
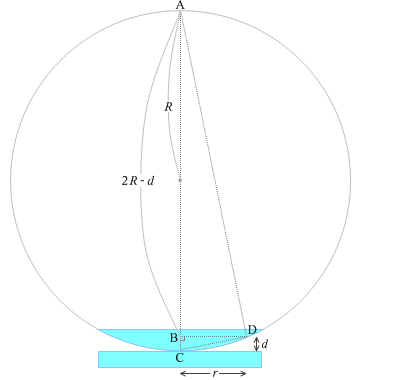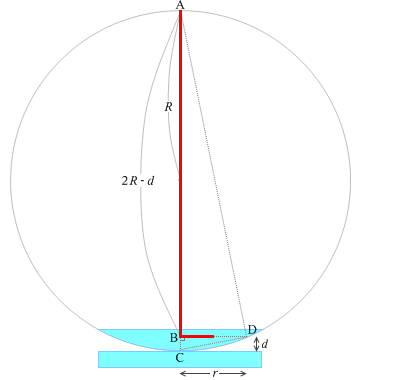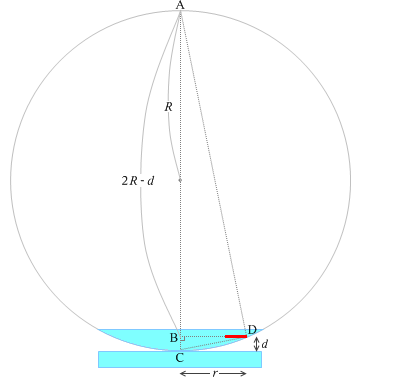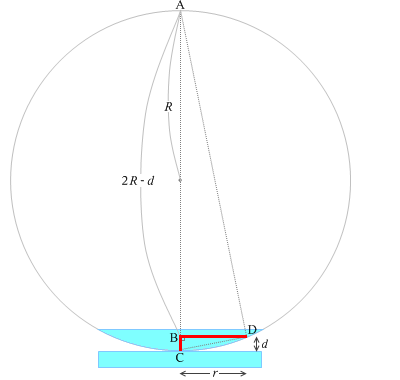平凸レンズの球面の曲率半径を \(R\) とし、ニュートンリングの縞の内の１つのリングの半径を \(r\) とし、空気層の厚さを \(d\) とし、左図のように符号を割り振ります。実際にニュートンリングが現れるときは \(d\) はとても小さく、\(d ≪ r,R\) です。このことを踏まえて光路差 \(2d\) を求めると、
△ABDと△DBCは相似だから
△ABDと△DBCが相似になるのはおわかりでしょうか。
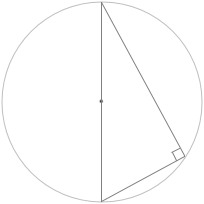円に内接する三角形のうち、円の中心を通るものは必ず直角三角形になります。
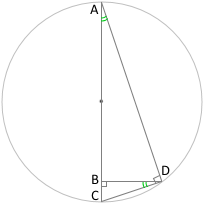
∠BADは、90° - ∠ADB
∠BDCも、90° - ∠ADB
つまり、∠BAD = ∠BDC
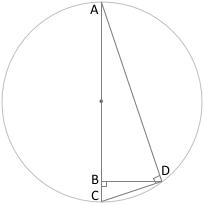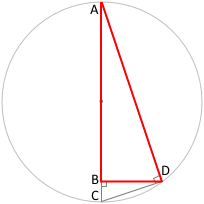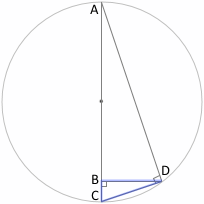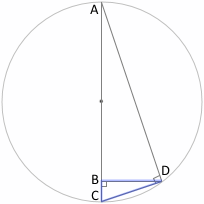
△ABDは、3つの角のうち1つの角が直角で、もう1つの角が∠BADです。
△DBCは、3つの角のうち1つの角が直角で、もう1つの角が∠BDCです。
2つの角が共通なので、△ABDと△DBCは相似です。
、
\((2R - d) : r = r : d\)
∴ \(r^2 = d(2R - d)\)
\(= 2dR - d^2\)
\(≒ 2dR\) (\(∵d ≪ R\))
よって、光路差 \(2d\) は、
\(2d ≒ {\large\frac{\ r^2}{R\ }}\)
下の平面ガラスの上面では固定端反射して位相が \(π\) ズレますので、光路差が (\(m + {\large\frac{1}{2}})λ\) のときに波が強め合います。（くさび形空気層の干渉とまったく同じです）。つまり \(2d = (m+\large{\frac{1}{2}})λ\) となる場所に、明るいリングができます。暗いリングができるのは \(2d = mλ\) となる場所です。
ニュートンリング
明るいリングの条件 \(\boldsymbol{{\large\frac{\ r^2}{R\ }} = (m + {\large\frac{1}{2}})λ}\)
暗いリングの条件 \(\boldsymbol{{\large\frac{\ r^2}{R\ }} = mλ}\)
\((m =0,1,2,…)\)
この式からレンズの曲率半径を求めたり、レンズの歪みなどを調べることができます。
\(m\) の値は、リングが中心から何番目のリングであるかを表しています。
また、ここまでは、上から当てる光は単色光（1種類の波長の光）であるとしてきましたが、白色光（あらゆる種類の波長を含む光）を当てた場合、1つひとつのリングが虹色に色づきます。波長 \(λ\) が異なると、上式において左辺の \(r\) が変わるからです。波長の大きい赤色はより外側にズレ、波長の小さい紫はより内側にズレます。