図1のように、\(x\)軸上の原点Oに電気量 \(Q\) の点電荷、\(x=d\) の位置に電気量 \(q\) の点電荷がそれぞれ固定されている。\(x=2d\) の位置の電場(電界)の大きさが 0 のとき、\(Q\) を表す式として正しいものを、下の①~⑥のうちから一つ選べ。
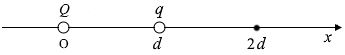
① \(4q\) ② \(2q\) ③ \(q\)
④ \(-q\) ⑤ \(-2q\) ⑥ \(-4q\)
#センター19本試物理
図1のように、\(x\)軸上の原点Oに電気量 \(Q\) の点電荷、\(x=d\) の位置に電気量 \(q\) の点電荷がそれぞれ固定されている。\(x=2d\) の位置の電場(電界)の大きさが 0 のとき、\(Q\) を表す式として正しいものを、下の①~⑥のうちから一つ選べ。
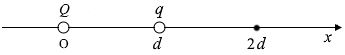
① \(4q\) ② \(2q\) ③ \(q\)
④ \(-q\) ⑤ \(-2q\) ⑥ \(-4q\)
#センター19本試物理
\(Q\) の点電荷が 2\(d\) の位置につくる電場と \(q\) の点電荷が 2\(d\) の位置につくる電場を合わせると 0 になるという話ですが、
まず \(Q\) の点電荷が 2\(d\) の位置につくる電場(\(E_Q\) とする)と求めますと
\(E_Q = k\large\frac{Q}{(2d)^2}\)
同様に、\(q\) の点電荷が 2\(d\) の位置につくる電場(\(E_q\) とする)は
\(E_q = k\large\frac{q}{d^2}\)
この2つを足して 0 になるということは \(Q\) は ⑥ \(-4q\) であるはずです。
(暗算で解くとすると)
電場が 0 になるということは \(Q\) と \(q\) は異符号であり、逆2乗の法則により倍だけ離れると強さは \(\large\frac{1}{4}\) になるので \(Q\) は \(q\) の4倍であるはずなので \(Q = -4q\) 、となります。