電場

電場とは

クーロンの法則

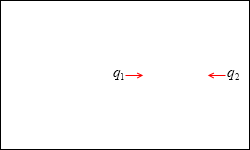
　　F = k\(\large{\frac{q_1q_2}{r^2}}\)

において、電荷 q₁ と電荷 q₂ が異符号（q₁×q₂ < 0）のとき、静電気力（クーロン力）の様子を図示すると、左図のようになります。

q₁ の位置が変わればこのようになったり、

このようになったりします。

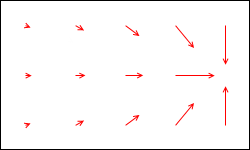q₁ にはたらく力をもっとたくさん描けば左図のようになります。

このように、なんらかの電荷（q₁）を置いたときに静電気力（クーロン力）が発生する空間を電場（あるいは電界）といいます。

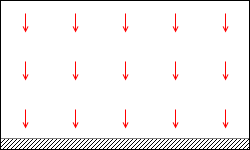これは、地表における重力を考えるときと似ています。＊重力がはたらく空間を重力場といいます。
　閉じる

でも、地表における重力は、向きが必ず鉛直下向きですし、その大きさはどの地点でも変わりません。（これは、質量が定まっている物体はどの地点においても重力の大きさが同じ、という意味です。重力加速度の大きさがどの地点でも同じということです）。

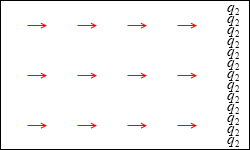地表における重力の例と電場の例を似させるのであれば、q₂ が平面状に分布している場合が適当かもしれません。

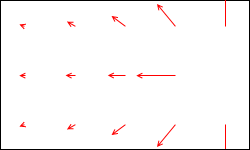また、q₁ と q₂ が同符号（q₁×q₂ > 0）のとき、静電気力の向き（電場の向き）はすべて逆向きになります。これについては重力と大きく異なるところです。

電場の大きさと向き

各地点の電場の大きさと向きというものを考えるとき、それは各地点の静電気力の大きさと向き、と同じだと考えられそうです、が、ちょっと違います。

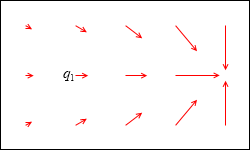クーロンの法則　F = k\(\large{\frac{q_1q_2}{r^2}}\)　によれば q₁ の大きさが大きくなると静電気力も大きくなりますし、

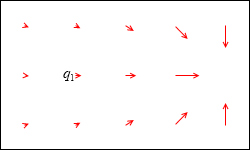q₁ の大きさが小さくなれば静電気力も小さくなります。

また q₁ の正負が逆転すれば静電気力の向きも逆転します。

ですので電場の大きさと向きというものを考えるときは、q₁ の大きさと正負の効果を取り除いたものを考えるのが妥当です。つまり、+1 C の電荷（正の単位電荷です。試験電荷、探り電荷などと呼ばれます。）をその地点に置いたときの静電気力を電場と定義する、のが妥当です。つまりそれは、静電気力を q₁ で割ったものです。

電場を \(\vec{E}\)＊Electric field の E閉じるで表し、q₁ を q に置き換えて表します。

これが電場の大きさ（強さ）で、向きは静電気力と同じ向きです（あるいは電荷が負であれば真逆の向きです）。単位は [N/C]（ニュートン毎クーロン）です＊あるいは [V/m] です。閉じる。たとえば、2N/C の電場に置かれた +3C の電荷は 6N の力を受けます。+4C の電荷なら 8N です。＊逆にいいますと、+3C の電荷が 6N の力を受けて、+4C の電荷が 8N の力を受けるような場所は、電場の強さが 2N/C になっています。
　閉じる

この電場というものは、地表における重力を考えたときの「重力加速度」に相当します。静電気力における \(\vec{E}\) は、重力における g です。

　　\(\vec{F}\) = q\(\vec{E}\)　は　F = mg　です。

g は方向が決まっているのでベクトルであることを強調しません。たいていベクトルの矢印を付けません。教科書によっては \(\vec{F}\) = q\(\vec{E}\) もベクトルの矢印を付けなかったりします。

点電荷のまわりの電場

クーロンの法則の式が

　　　　F = k\(\large{\frac{q_1q_2}{r^2}}\)

であり、これを q₁ で割った

　　　　E = \(\large{\frac{F}{q_1}}\)

が電場であると説明しましたが、であるならば電場は、

　　　　E = \(\large{\frac{F}{q_1}}\) = \(\large{\frac{k\frac{q_1q_2}{r^2}}{q_1}}\) = \(k\large{\frac{q_2}{r^2}}\)

という風にも表現することができるわけです。

そして、そもそもの定義では、q₁、q₂ は荷電粒子（=点電荷）であったわけです。としますと上式は、「点電荷 q₂ のまわりの電場の式」と解釈できます。（もし q₂ が点電荷でない場合は、おおもとのクーロンの法則自体が成り立ちません。＊棒状電荷だったり板状電荷だったりしてもそれが点電荷の集合体であると考えればクーロンの法則は成り立っていますが…
　閉じる）

q₂ を q に置き換えて表しますと以下のようになります。

この式は、q [C] の点電荷から r [m] だけ離れた地点の電場の強さ、を表します。q の正負が入れ替われば電場の向きも入れ替わります。

電場の和

静電気力（クーロン力）は足し合わせることができます。

たとえば、q₁ [C]、q₂ [C]、q₃ [C] の３つの点電荷があるとき、q₁ の電荷にはたらく力は、q₂ からの力と q₃ からの力の合力となります。q₁ q₂間を r₂ [m]、q₁ q₃間を r₃ [m] としますと、q₁ にはたらく力は以下のように表せます。

　　　　F = k\(\large{\frac{q_1q_2}{r_2{^2}}}\) + k\(\large{\frac{q_1q_3}{r_3{^2}}}\)

足し合わせることができることを、重ね合わせることができる、線形である、といったりもします。

このときの電場は、

　　　　E = \(\large{\frac{F}{q_1}}\) = \(\large{\frac{k\frac{q_1q_2}{r_2{^2}}}{q_1}}\) + \(\large{\frac{k\frac{q_1q_3}{r_3{^2}}}{q_1}}\) = \(k\large{\frac{q_2}{r_2{^2}}}\) + \(k\large{\frac{q_3}{r_3{^2}}}\) = E₂ + E₃

となり、電場も足し合わせられることが証明されます。

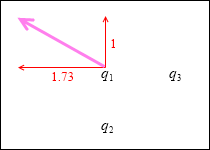しかし、力も電場もベクトルでありますので、ベクトルの加法にのっとって足し合わせなければなりません。

1N/C の電場と 1.73N/C の電場を単純に足し合わせて 2.73N/C 、とやってはいけません。左図の例でいえば、2.73 でなく 約2N/C となります。（一方の角が 30° の直角三角形の辺の比は　1 : 約1.73 : 2　です）

E をベクトル表記に直して、さらに E₂ を \(\vec{E}_1\) 、E₃ を \(\vec{E}_2\) に置き換えて表現し直しますと、

となります。