qOA85

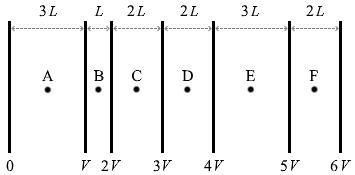
図3のように互いに平行な極板が、\(L\)、\(2L\)、\(3L\) の3通りの間隔で置かれており、左端の極板の電位は 0 で、極板の電位は順に一定値 \(V\)（>0）ずつ高くなっている。隣り合う極板間の中央の点A～Fのいずれかに点電荷を1つ置くとき、点電荷にはたらく静電気力の大きさが最も大きくなる点または点の組合せとして最も適当なものを、下の①～⑨のうちから一つ選べ。ただし、点電荷が作る電場（電界）は考えなくてよい。

図 3

①　A　　　 ②　B　　　 ③　C

④　D　　　 ⑤　E　　　 ⑥　F

⑦　CとDとF　⑧　AとE　⑨　すべて

#共テ21本試物理

点電荷にはたらく静電気力の大きさは電場の強さ（\(E\)）によります。平行な極板による電場は一様なものになりますが、このときの電位（\(V\)）は電場の強さ（\(E\)）と距離（\(d\)）を掛けたものです。

　　\(V = Ed\)

です。変形すると

　　\(E = \large\frac{V}{d}\)

です。これをグラフで表しますと、

このようになります。

赤線の傾きが電場の強さです。

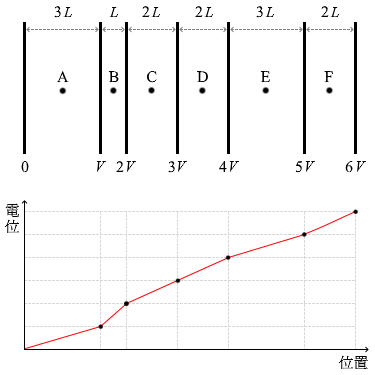つまり静電気力が最も大きくなる点は ② B です。