電位

静電気力による位置エネルギー

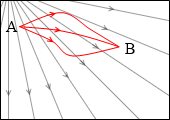静電気力は保存力です。電荷が電場の中をどのような経路で進んで行っても、その仕事は同じです。重力や弾性力と同様です。

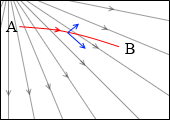A点からB点に進むとき、電場の方向に進む成分と電場に垂直な方向に進む成分に分けられますが、電場に垂直に進む成分は力を受けません。静電気力は電場の方向のみにはたらくものです。

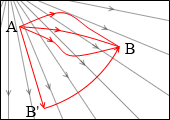よって、どんな経路をたどろうとも、それは A点→B’点→B点 と進むのと一緒です。（A点→B’点を進むときだけ力を受けて、B’点→B点を進むときは力を受けません。）

保存力がはたらいて非保存力（摩擦力など）がはたらかない空間においては、経路は問題にならず、位置だけが問題になります。

保存力のみが発揮される空間においては、位置だけで決まるエネルギーがあるとみなせます。（『重力による位置エネルギー』、『弾性力による位置エネルギー』、『万有引力による位置エネルギー』参照）

一様な電場での位置エネルギー

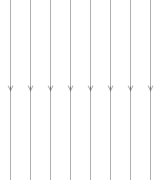一様な電場での位置エネルギーを考えてみます。一様な電場というのは、電荷をどの地点に置いても、同じ方向、同じ大きさの静電気力が発生するような電場です。

位置エネルギーの量というものは、基準の位置から電荷を動かすときの仕事の量のことです。仕事の量というのは、受けた力と移動した距離を掛け合わせたものです。

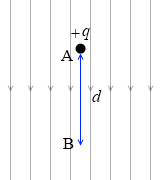一様な電場 E [N/C] に置かれた +q [C] の電荷は qE [N] の力を受けます。この電荷が d [m] 進むと、そのときの仕事 W [J] は ＊ このときの「仕事」には２つの考え方があります。
A点からB点に下ろしたときの、静電気力が電荷に対してした仕事、という考え方と、
B点からA点に持ち上げるときの、外力（たとえば手など）が静電気力に逆らってした仕事、という考え方です。
教科書によって説明方法が違うかもしれませんが、どちらも同じです。
このとき、「静電気力」も「手」も力の大きさは同じです。つり合っていますので…。「仕事」について考えるときはゆっくり動かし、つり合った状態をキープします。ですから力の大きさは同じです。
「正負」が違うのではないかと思ってしまうかもしれませんが、それも同じです。静電気力が電荷を動かす場合、静電気力は下向きですし、電荷の動く方向も下向きです。よってその積は「正」です。手が電荷を動かす場合、手の力の向きは上向きで、電荷の動く方向も上向きです。よってその積は「正」です。つまりどちらの場合も「正」です。
　閉じる

　　W = qE×d

です。ですので、B点を基準としたときのA点の位置での電荷の位置エネルギー U は

　　U = qEd

です。

このように「一様な電場」においては静電気力による位置エネルギーは簡単に求められます。

そして、この値は地表付近の重力による位置エネルギー mgh とそっくりです。mgh と qEd を見比べてみますと、

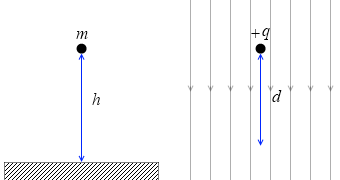　　m ⇔ q
　　g ⇔ E
　　h ⇔ d

という対応が考えられ、h が大きいほど、d が大きいほど、位置エネルギーが大きくなる、といえます。

…と、ここまではいいのですが、電場というものは「一様」とは限らず、

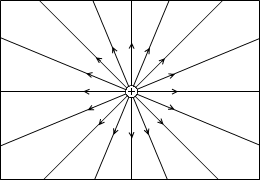このようであったり、

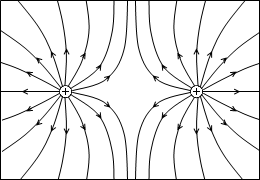このようであったりします。

地表付近の「重力場」の場合は g の大きさと向きが一定なので、h が大きければ位置エネルギーも大きい、と話が単純でいいのですが、「電場」の場合は E の大きさと向きが一定とは限りません。ですので、d が大きいからといって位置エネルギーが大きいとはいえません。d が位置エネルギーの目安にならないのです。

そこで、Ed という量を目安にします。電荷をある電場に置いたときに、その位置の Ed の値が大きければ確実に位置エネルギーも大きいですし、Ed が小さければ確実に位置エネルギーも小さいです。（ Ed は mgh のうちの gh にたとえることができます。）

電位

Ed を電位といい、量記号 V で表します。

単位は [V] ボルト です。量記号も V ですし単位も V です。V [V] です。＊量記号と単位が同じ記号という珍しいパターンです。量記号は斜字体、単位は立体で表記します。語源は18世紀のイタリアの物理学者 Alessandro Volta アレッサンドロ・ボルタ から。volt 、voltage が語源とも考えられます。
ジャマイカの陸上選手は Usain Bolt です。こちらはボルトとナットのboltと同じです。
　閉じる

この電位 V = Ed を上で示した

　　　　U = qEd

の式に代入してみますと、

　　　　U = qV

となります。この式を解釈しますと、V [V] の電位のところに置かれた q [C] の電荷の位置エネルギーは U [J] である、ということになります。

さらにいいますと、q が +1 C のとき U = V となります。つまりこれは、電位というのは +1 C の電荷（正の単位電荷）の位置エネルギーのことである、といえます。

単位について考えてみますと、

ということがいえます。

そして、この位置エネルギーの基準点なのですが、（位置エネルギーの基準はどこでもいいのですが）、無限遠の彼方（大本となる電荷の影響が及ばない点）や地面（地球は無尽蔵に電荷を吸収するとみなせる）とすることが多いです。電気回路の場合、考えやすくなる点を基準とすることが多いです。

電位差

重力による位置エネルギーの基準といえば大抵、地表のことです。しかし電気回路等での電位の基準はどこにすればいいか絶対的なものがありません。ですので、基準と比べた値というより、2点間の差というものを意識します。

その電位と電位の差を電位差といいます。あるいは電圧といいます。

q [C] の電荷を運ぶとき、2点間の電位差が V [V] であれば、その仕事 W は W = qV [J] です。

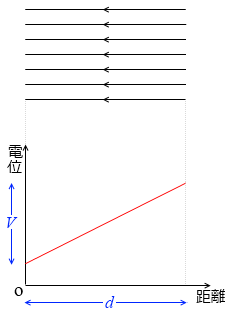そのときの電場 E [V/m] が一様な電場であれば、2点間の距離 d [m] を使って

　　　　V = Ed

と表され、E は（横軸を距離、縦軸を電位としたグラフの）曲線の傾きを示していることになります。