qG93A

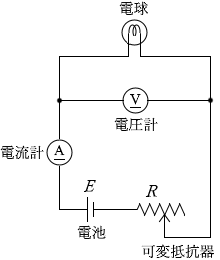
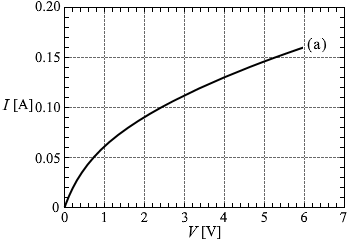
電球にかかる電圧と流れる電流の関係を調べるため、図3のような回路(a)を組んだ。可変抵抗器の抵抗値を変えながら、電圧計の値 V [V] と電流計の値 I [A] を読みとり、図4の結果を得た。ただし、電池および電流計の内部抵抗と電圧計に流れる電流は無視できるものとする。

図 3　回路(a)
図 4

（問3）回路(a)で、電池の起電力 E [V] 、可変抵抗器の抵抗値が R [Ω] のとき、V と I の間に成り立つ関係として正しいものを、次の①～④のうちから一つ選べ。

①　V = - E + RI　　②　V = - E - RI
③　V = E - RI　　　④　V = E + RI

（問4）回路(a)で、起電力 E = 6.0 V 、可変抵抗器の抵抗値 R = 30 Ω のときの電圧の測定値 V はいくらか。最も適当なものを、次の①～⑥のうちから一つ選べ。

①　1.6　　②　2.0　　③　2.4
④　2.8　　⑤　3.2　　⑥　3.6

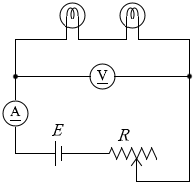
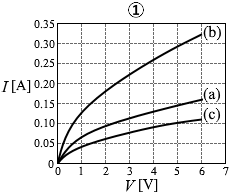
（問5）回路(a)と同じ電球2個を直列につないだ回路(b)(図5)、並列につないだ回路(c)(図6)を考える。回路(a)のときと同じように、電圧計と電流計を用いて、回路(b)、回路(c)について電圧と電流の関係を調べた。これらの結果を回路(a)の結果と共に表すと、どのようなグラフが得られるか。最も適当なものを、次の①～⑥のうちから一つ選べ。

図 5　回路(b)
図 6　回路(c)
　　　　　　

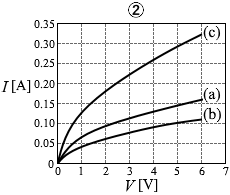
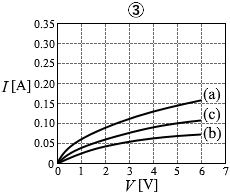
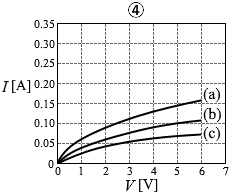
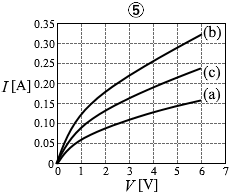
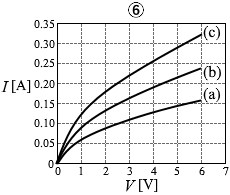
#センター01本試

（問3）
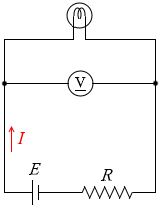回路図を簡潔に描くと左図のようになり、

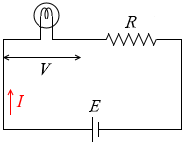さらに簡潔に描くと左図のようになり、

電位差の関係は、

　　E = V + RI

であり、

つまり、③ V = E - RI です。

　

（問4）
与えられた E と R の値を、問3で求めた　V = E - RI　式に代入しますと、

　　　　V = 6.0 - 30×I

求める V は、この式と図4のグラフを同時に満たすはずだから、この式の曲線をグラフに描き込んで交点を探ると、

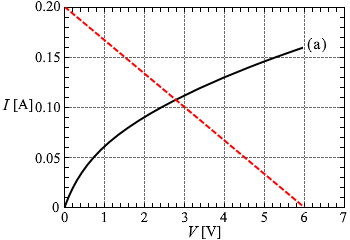（ V = 6.0 - 30×I　は、V = 0 のとき I = 0.20 、I = 0 のとき V = 6.0 の直線 ）

V がだいたい 2.8 くらいのところで交わります。

答えは ④ 2.8 [V]

（ I は 0.10666 [A] くらいです。）

　

（問5）

回路(b)では電球が直列につながれていますので、回路(a)と比べると、同じ電流が流れるときに電圧の大きさが2倍になります。

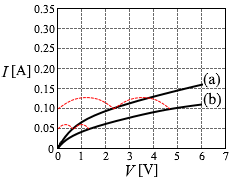そのようになっているグラフは②か④です。

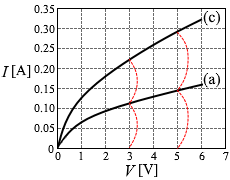回路(c)では電球が並列につながれています。それぞれの電球には同じ電圧が掛かります。個々の電球には回路(a)のときと同じ電流が流れます。電流計にはそれらが足し合わされた電流が流れます。つまり、回路(a)と比べると、同じ電圧が掛かるときに電流の大きさは2倍となります。

そのようになっているグラフは②か⑥です。

というわけで答えは ② です。

↑ ↓