qG875

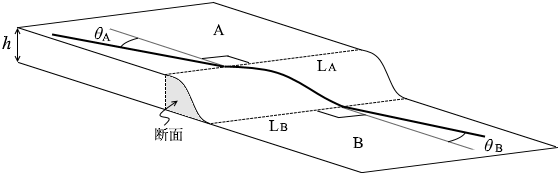
図2のように、水平面A、Bが、高さ h の斜面台をはさんで、なめらかにつながっている。平面と斜面台の交線L_A、L_Bは互いに平行で、交線に垂直な斜面台の断面の形は場所によらず同じである。交線L_Aに垂直に交わる直線と角度 θ_A をなす方向から、質量 m の小物体が速さ V_A で等速直線運動をしてきて、斜面を通過し、平面Bに到達した。平面B上では、小物体は交線L_Bに垂直に交わる直線と角度 θ_B をなす方向に速さ V_B で等速直線運動をした。小物体と面との間に摩擦はなく、また、小物体は面から離れることなく運動する。ただし、重力加速度の大きさを g とする。

図 2

（問3）平面B上での小物体の速さ V_B はいくらか。

（問4）速さ V_A 、V_B および角度 θ_A 、θ_B の間の関係として正しいものを、次の①～⑤のうちから一つ選べ。

① V_A = V_B 、θ_A = θ_B　　② V_Asinθ_A = V_Bcosθ_B

③ V_Acosθ_A = V_Bsinθ_B　　④ V_Asinθ_A = V_Bsinθ_B

⑤ V_Acosθ_A = V_Bcosθ_B

（問5）小物体の運動量の鉛直上向き成分 p_z の時間変化を表すグラフとして最も適当なものを、次の①～⑥のうちから一つ選べ。

　　　　　　

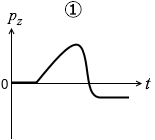
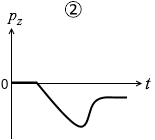
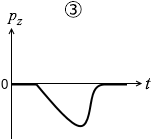
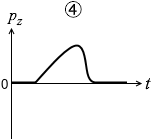
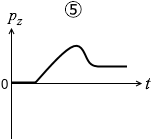
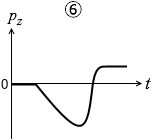
#センター05本試

（問3）
平面A上を運動中の力学的エネルギーは

　　　　\(\large{\frac{1}{2}}\)mV_A² + mgh

平面B上を運動中の力学的エネルギーは

　　　　\(\large{\frac{1}{2}}\)mV_B² + mg⋅0

力学的エネルギー保存の法則よりこの2つは等しいから、

　　　　\(\large{\frac{1}{2}}\)mV_A² + mgh = \(\large{\frac{1}{2}}\)mV_B²

　∴　　V_A² + 2gh = V_B²

　∴　　V_B = \(\sqrt{{V_A}^2+2gh}\)

　

（問4）

問題文の「平面と斜面台の交線L_A、L_Bは互いに平行で、交線に垂直な斜面台の断面の形は場所によらず同じである。」というのは、斜面がかまぼこ型というか巻きずし型になっているということです。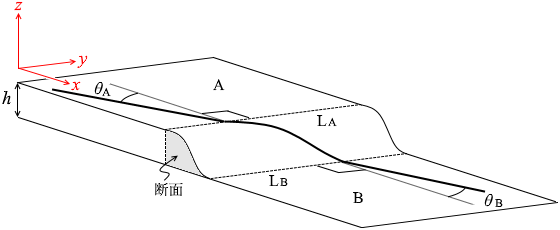

左図のように xyz軸を設定しますと、

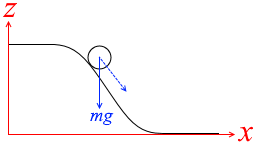斜面を下る小物体にはたらく力は重力の斜面方向成分ですが、この力は x-z平面内に収まっていて、

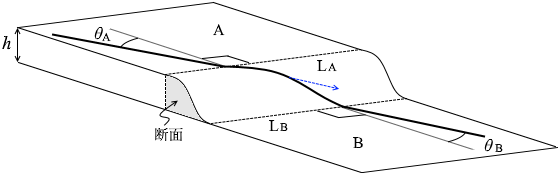決して y方向にははみ出しません。

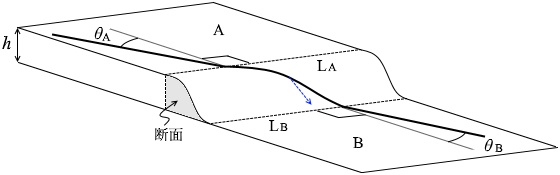常にx-z平面内に収まっています。

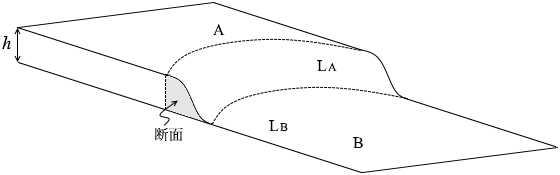もし斜面がすり鉢状であったりすれば y方向にはみ出しますが、今回はそうではありません。

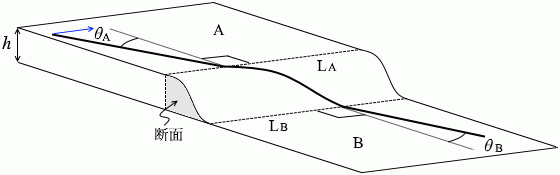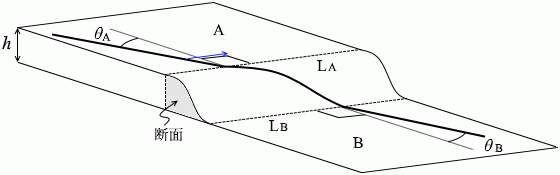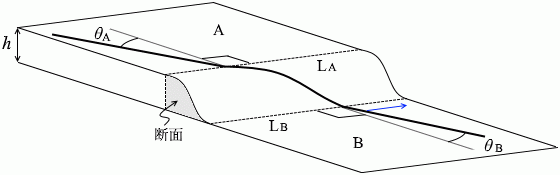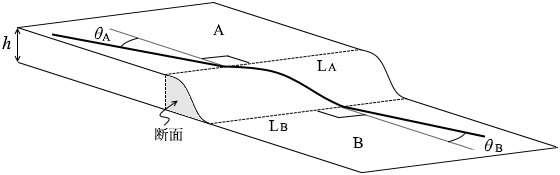というわけで、速度の y成分は最初から最後まで変化することはありません。

（V_A から V_B へ速度が増すのは x成分だけです）

平面Aでの速度の y成分は V_Asinθ_A であり、平面Bでの速度の y成分は V_Bsinθ_B であり、よって、

　　　　V_Asinθ_A = V_Bsinθ_B

です。答えは ④ です。

　

この問題は、運動や力を3次元の各成分にちゃんと分解できるかを問いただしています。

（問5）小物体の運動量の鉛直上向き成分 p_z の時間変化を表すグラフとして最も適当なものを、次の①～⑥のうちから一つ選べ。

　　　　　　

運動量とは質量と速度を掛けたものであり、いまの場合、質量は一定だから、実質的に速度の変化の具合を聞かれていることになります。

平面A上、平面B上を運動中は速度の鉛直成分（z成分）は 0 です。そうなっているグラフは ③ か ④ です。

そして、上向きが正であるので、斜面台上を運動中の速度は負です。そうなっているグラフは ③ です。

↑ ↓