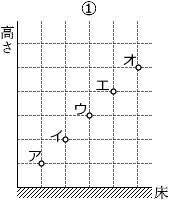
5個の小球ア~オを時刻 t = 0 で異なる高さから初速度 0 で同時に落下させたところ、t = 0 から等しい時間間隔で、小球が順に床に衝突した。t = 0 で、それぞれの小球はどのような高さにあったか。最も適当なものを、次の①~④のうちから一つ選べ。ただし、空気抵抗は無視できるものとする。
#センター03本試
5個の小球ア~オを時刻 t = 0 で異なる高さから初速度 0 で同時に落下させたところ、t = 0 から等しい時間間隔で、小球が順に床に衝突した。t = 0 で、それぞれの小球はどのような高さにあったか。最も適当なものを、次の①~④のうちから一つ選べ。ただし、空気抵抗は無視できるものとする。




#センター03本試
この問題の題意は、
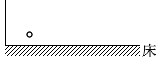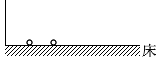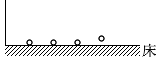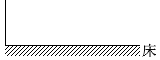 床に衝突する時間間隔がトン、トン、トン、トン、トンとリズムよく等間隔になるには、スタート位置をどのように配置すればいいか、ということです。
床に衝突する時間間隔がトン、トン、トン、トン、トンとリズムよく等間隔になるには、スタート位置をどのように配置すればいいか、ということです。
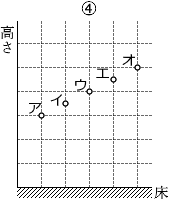
物体が等速で進んで行くなら①か④のグラフが正解でしょうが、落下していく物体は重力によって加速されますから、そんな単純ではありません。
アの小球がスタートしてから床に衝突するまでの時間を T と置きますと、
イの小球のスタートから衝突までの時間は 2T で、
ウの小球のスタートから衝突までの時間は 3T で、
エの小球のスタートから衝突までの時間は 4T で、
オの小球のスタートから衝突までの時間は 5T です。
そして、自由落下運動の変位の式 y = \(\large{\frac{1}{2}}\)gt2 より、
スタートから着地まで物体が T秒間に落下する距離は \(\large{\frac{1}{2}}\)gT2 [m]
スタートから着地まで物体が 2T秒間に落下する距離は \(\large{\frac{1}{2}}\)g(2T)2 = 4×\(\large{\frac{1}{2}}\)gT2 [m]
スタートから着地まで物体が 3T秒間に落下する距離は \(\large{\frac{1}{2}}\)g(3T)2 = 9×\(\large{\frac{1}{2}}\)gT2 [m]
スタートから着地まで物体が 4T秒間に落下する距離は \(\large{\frac{1}{2}}\)g(4T)2 = 16×\(\large{\frac{1}{2}}\)gT2 [m]
スタートから着地まで物体が 5T秒間に落下する距離は \(\large{\frac{1}{2}}\)g(5T)2 = 25×\(\large{\frac{1}{2}}\)gT2 [m]
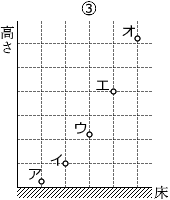
高さの比率がこのように並んでいるのは ③ のグラフです。
ちなみに T = 1 [秒] としますと、
1秒で落下する距離 \(\large{\frac{1}{2}}\)×9.8×12 = 4.9 [m]
2秒で落下する距離 \(\large{\frac{1}{2}}\)×9.8×22 = 19.6 [m]
3秒で落下する距離 \(\large{\frac{1}{2}}\)×9.8×32 = 44.1 [m]
4秒で落下する距離 \(\large{\frac{1}{2}}\)×9.8×42 = 78.4 [m]
5秒で落下する距離 \(\large{\frac{1}{2}}\)×9.8×52 = 122.5 [m]
となります。30階建てのビルの屋上から鉄球を落下させると 5秒くらいで着地します。
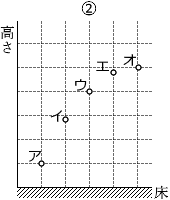
あと、②について考えてみますと、これは、始めに同じ高さに配置した5つの小球を等しい時間間隔でスタートさせていった場合の落下途中の様子を表すグラフとなっています。