電車の運転席には様々な計器がある。電車がA駅を出発してからB駅に到着するまで、電車の速さ \(v\)、電車の駆動用モーターに流れた電流 \(I\)、モーターに加わった電圧 \(V\) を 2s ごとに記録したデータがある。図1は \(v\) と時刻 \(t\) の関係を、図2は \(I\) と \(t\) の関係をグラフにしたものである。電流が負の値を示しているのは、電車のモーターを発電機にして運動エネルギーを電気エネルギーに変換しているためである。A駅とB駅の間の線路は、地図上では直線である。車両全体の質量は 3.0×104kg であり、重力加速度の大きさを 9.8m/s2 とする。
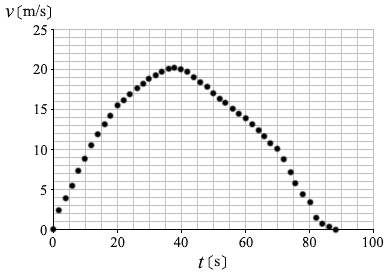
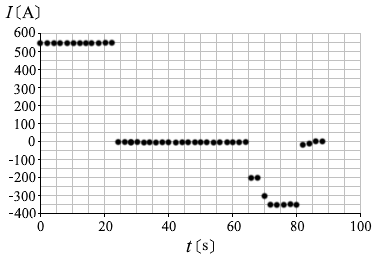
（問1）qO3L7
（問2）qO3L7
（問3）qO3L8
（問4）\(t\) = 40s から \(t\) = 60s の区間で、電車は勾配のある線路上を運動していた。摩擦や空気抵抗の影響を無視し、力学的エネルギーが保存されるものとすると、この区間の高低差はおよそ 何m か。最も適当な数値を、次の①～⑤のうちから一つ選べ。
① 1 ② 5 ③ 10 ④ 20 ⑤ 30
#共テ21追試物理基礎
（問4）図2を見てみますと \(t\) = 25s くらいから \(t\) = 65s くらいまで電流 \(I\) が 0 なので駆動用モーターは動いていないとわかります。そして図1を見てみますと \(t\) = 25s くらい以降加速していて \(t\) = 38s くらい以降から減速をしています。これは \(t\) = 25s くらいから下り坂で、 \(t\) = 38s くらい以降は上り坂ということです。そしてこの間駆動用モーターは動いていないので力学的エネルギーが保存されているわけです。
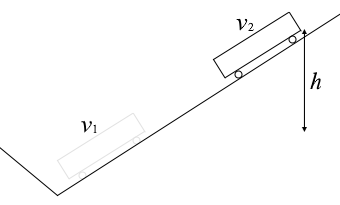電車の質量を \(m\)、\(t\) = 40s での速さを \(v_1\)、\(t\) = 60s での速さを \(v_2\)、高低差を \(h\) としますと、
\(t\) = 40s での電車の力学的エネルギーは
\({\large\frac{1}{2}}mv{_1}^2\)
\(t\) = 60s での電車の力学的エネルギーは
\({\large\frac{1}{2}}mv{_2}^2 + mgh\)
力学的エネルギー保存の法則よりこの2つは等しいから
\({\large\frac{1}{2}}mv{_1}^2 = {\large\frac{1}{2}}mv{_2}^2 + mgh\)
∴ \({\large\frac{1}{2}}v{_1}^2 = {\large\frac{1}{2}}v{_2}^2 + gh\)
図1から読み取った数値、\(v_1\) = 20、\(v_2\) = 14、重力加速度 \(g\) = 9.8 を代入すると、
\({\large\frac{1}{2}}20^2 = {\large\frac{1}{2}}14^2 + 9.8h\)
∴ 10 × 20 = 7 × 14 + 9.8\(h\)
∴ 9.8\(h\) = 200 - 98
∴ \(h\) = \(\large\frac{102}{9.8}\)
選択肢の中で最も近いのは ③ 10 です。