qO5S6

小球の運動について問いに答えよ。ただし、空気抵抗は無視できるものとする。

　

図1は、ある初速度で水平右向きに投射された小球を、0.1s の時間間隔で撮影した写真である。壁には目盛り間隔 0.1m のものさしが水平な向きと鉛直な向きに固定されている。

図 1

　

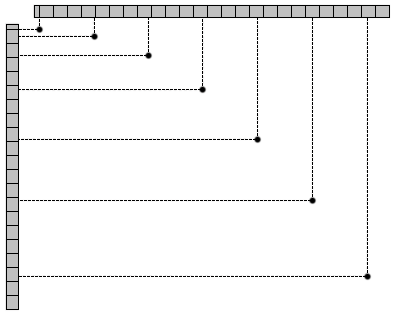
（問1）qO5S5
（問2）qO5S5

　

（問3）次の文章中の空欄7・8に入れる記述として最も適当なものを、それぞれの直後の｛ ｝で囲んだ選択肢のうちから一つずつ選べ。

図1の水平投射の実験を実験ア、初速度の大きさを実験アより大きくして水平投射させた実験を実験イ、初速度の大きさを実験アより小さくして水平投射させた実験を実験ウとよぶ。同じ質量の三つの小球を使って実験ア、実験イ、 実験ウを同じ高さから同時に行い、三つの小球を水平な床に到達させた。このとき、

7 ｛ ① 実験アの小球が最も早く　② 実験イの小球が最も早く　③ 実験ウの小球が最も早く　④ 実験ア、実験イ、実験ウの小球が同時に ｝ 床に到達した。

また、床に到達したときの速さを比べると、力学的エネルギー保存の法則より、

8 ｛ ① 実験アの小球の速さが最も大きい。　② 実験イの小球の速さが最も大きい。　③ 実験ウの小球の速さが最も大きい。　④ 実験ア、実験イ、実験ウの小球の速さはすべて等しい。 ｝

#共テ23本試物理基礎

7
初速度の大きさをいろいろ変えたとしてもそれは水平方向に関わる速度であり鉛直方向の速度には無関係です。床に到達するまでの時間は鉛直方向の速度のみによって決まり、実験アでも実験イでも実験ウでも到達時間は変わりません。答えは ④ 実験ア、実験イ、実験ウの小球が同時に です。

　

　

8
小球の質量を \(m\) 、床に到達したときの速さを \(v\) 、初速度の大きさを \(v_0\) 、床からスタート地点までの高さを \(h\) 、重力加速度の大きさを \(g\) として、小球の力学的エネルギー保存の法則の式を立てますと

　　\({\large\frac{1}{2}}mv_0{^2} + mgh = {\large\frac{1}{2}}mv^2\)

∴　\(v_0{^2} + 2gh = v^2\)

∴　\(v = \sqrt{v_0{^2} + 2gh}\)

となり、初速度が大きいほど床に到達したときの速さが大きいとわかります。

答えは ② 実験イの小球の速さが最も大きい。 です。

　

（別解）
到達したときの速度を鉛直方向と水平方向に分解したときに、鉛直方向は実験ア、実験イ、実験ウとも同じで、水平方向は初速度によります。つまり初速度が大きい実験がトータルで一番大きくなり、それは実験イです。