水平投射

水平投射 基礎物理範囲

水平方向に初速を与えて、あとは重力の力にまかせて落下させるような運動を水平投射といいます。

自由落下運動、鉛直投射との大きな違いは、1次元の運動であるか、2次元の運動であるか、という点です。水平投射は2次元の運動であり、一見複雑なのですが、重力というものは方向が常に鉛直下向きであり、運動を水平方向と鉛直方向に分解しますと、重力加速度を考えるのは鉛直方向だけでよく、かなり単純化されます。物理では2次元を1次元に分解して考えることがよくあります。

水平投射。

横軸の x軸に着目すると、速度が初速度のまま一定の等速直線運動。

縦軸の y軸に着目すると速度は増している。これはまさに自由落下運動。

水平投射を表す式 物理範囲

初速度を v₀ 、x軸方向の速度を v_x 、y軸方向の速度を v_y とします。

x軸方向には、速度が初速度のまま一定の等速直線運動をするから、

　　　　速度　v_x = v₀　　（一定）

　　　　位置　x = v₀ t

y軸方向には、自由落下運動をするから、鉛直下向きを正として、

　　　　速度　v_y = g t

　　　　位置　y = \(\large{\frac{1}{2}}\) g t²

さらに、x = v₀ t　を　y = \(\large{\frac{1}{2}}\) g t²　に代入して t を消去すると、

　　　　y = \(\large{\frac{1}{2}}\) g \(\bigl(\large{\frac{x}{v_0}}\bigr)^2\)

　　　　　= \(\large{\frac{g}{2{v_0}^2}}\) x²

これは水平投射した物体の軌道を表す式であり、y = (定数)・x²　の形になっているので x の2次関数であり、グラフの曲線は放物線になります。いま、鉛直下向きを正としていますので、上に凸の放物線になります＊(定数)の部分が正ですので普通の2次関数の場合は下に凸の放物線のはずですが、今は下向きを正としているので逆になります。あと、放物線の頂点は原点になります。詳しくは数学の教科書を見てください。
　閉じる。

この水平投射における速度ベクトルの大きさ、つまり速さを求めてみますと、

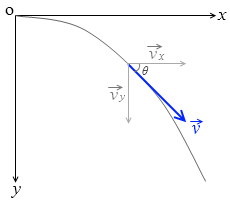　　v = \(\sqrt{{v_x}^2+{v_y}^2}\) = \(\sqrt{{v_0}^2+(gt)^2}\)

また、この速度ベクトルの角度は、水平とのなす角（俯角＊ふかく。うつむく角。

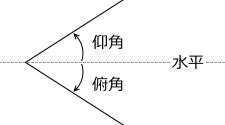
　 閉じる）を θ とすると、

　　tanθ = \(\large{\frac{v_y}{v_x}}\) = \(\large{\frac{gt}{v_0}}\)

となります。