小球の運動について問いに答えよ。ただし、空気抵抗は無視できるものとする。
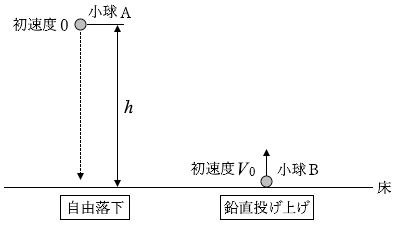
同じ質量の二つの小球A、Bを用意した。図2のように、水平な床を高さの基準面として、小球Aを高さ \(h\) の位置から初速度0で自由落下させると同時に、小球Bを床から初速度 \(V_0\) で鉛直に投げ上げたところ、小球A、Bは同時に床に到達した。
(問4)\(V_0\) を、\(h\) と重力加速度の大きさ \(g\) を用いて表す式として正しいものを、次の①~⑥のうちから一つ選べ。
① \(\sqrt{\large\frac{h}{g}}\) ② \(\sqrt{\large\frac{g}{h}}\) ③ \(\sqrt{gh}\) ④ \(\sqrt{\large\frac{h}{2g}}\) ⑤ \(\sqrt{\large\frac{g}{2h}}\) ⑥ \(\sqrt{\large\frac{gh}{2}}\)
(問5)次の文章中の空欄ア・イに入れる式の組合せとして正しいものを、後の①~⑨のうちから一つ選べ。
床に到達する時点での小球A、Bの運動エネルギー \(K_{\rm{A}}\) 、\(K_{\rm{B}}\) の大小関係は、計算をせずとも以下のように調べられる。
小球Bの最高点の高さを \(h_{\rm{B}}\) とする。運動を開始してから床に到達するまでの時間は小球A、Bで等しいことから、\(h\) と \(h_{\rm{B}}\) の大小関係はアであることがわかる。小球が最高点から床に達する間に失った重力による位置エネルギーは、床に到達する時点で運動エネルギーにすべて変換されるので、\(K_{\rm{A}}\) と \(K_{\rm{B}}\) の大小関係はイであることがわかる。
| ア | イ | |
|---|---|---|
| ① | \(h = h_{\rm{B}}\) | \(K_{\rm{A}} > K_{\rm{B}}\) |
| ② | \(h = h_{\rm{B}}\) | \(K_{\rm{A}} < K_{\rm{B}}\) |
| ③ | \(h = h_{\rm{B}}\) | \(K_{\rm{A}} = K_{\rm{B}}\) |
| ④ | \(h < h_{\rm{B}}\) | \(K_{\rm{A}} > K_{\rm{B}}\) |
| ⑤ | \(h < h_{\rm{B}}\) | \(K_{\rm{A}} < K_{\rm{B}}\) |
| ⑥ | \(h < h_{\rm{B}}\) | \(K_{\rm{A}} = K_{\rm{B}}\) |
| ⑦ | \(h > h_{\rm{B}}\) | \(K_{\rm{A}} > K_{\rm{B}}\) |
| ⑧ | \(h > h_{\rm{B}}\) | \(K_{\rm{A}} < K_{\rm{B}}\) |
| ⑨ | \(h > h_{\rm{B}}\) | \(K_{\rm{A}} = K_{\rm{B}}\) |
#共テ23本試物理基礎