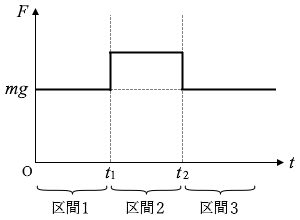
図2のように、質量 \(m\) のおもりに糸を付けて手でつるした。時刻 \(t\)=0 でおもりは静止していた。おもりが糸から受ける力を \(F\) とする。鉛直上向きを正として、\(F\) が図3のように時間変化したとき、おもりはどのような運動をするか。0 < \(t\) < \(t_1\) の区間1、\(t_1\) < \(t\) < \(t_2\) の区間2、\(t_2\) < \(t\) の区間3の各区間において、運動のようすを表した下記の文の組合せとして最も適当なものを、下記の①～⑦のうちから一つ選べ。ただし、重力加速度の大きさを \(g\) とし、空気抵抗は無視できるものとする。
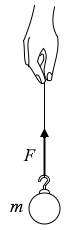
a 静止している。
b 一定の速さで鉛直方向に上昇している。
c 一定の加速度で速さが増加しながら鉛直方向に上昇している。
d 一定の加速度で速さが減少しながら鉛直方向に上昇している。
| 区間1 | 区間2 | 区間3 | |
|---|---|---|---|
| ① | a | b | a |
| ② | a | b | d |
| ③ | a | c | a |
| ④ | a | c | b |
| ⑤ | b | c | a |
| ⑥ | b | c | b |
| ⑦ | b | c | d |
#共テ22本試物理基礎
（区間1）
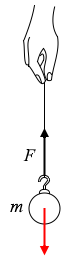質量 \(m\) のおもりには重力が \(mg\) だけ掛かりますから、時刻 \(t\)=0 で静止していたということは \(F\) の大きさが \(mg\) でつり合っていたということです。図3のグラフの曲線もそうなっています。\(t_1\) までの間この \(F\) の大きさは変わらないのだから、この間おもりは 静止 していたということになります。
（区間2）
その後、\(F\) が大きくなるので、これはつまり 鉛直上向きに加速した ということです。これは \(t_2\) までの間続いたということです。
（区間3）
その後、\(F\) の大きさが \(mg\) に戻ったのだから再びおもりは静止した、、、と考えてしまうと間違いです。おもりは静止しません。下向きの力と上向きの力が同じになってつり合ったからといって静止するわけではありません。慣性の法則によれば、物体にはたらく合力が 0 であるとき（つり合っているとき）、運動している物体はそのまま等速度運動を続けます。 \(t_2\) の段階でおもりには鉛直上向きの初速がついています。その 初速のまま上向きに運動し続ける のです。初速がついていて、下向きの力と上向きの力がちょうど同じになっていて、そのまま等速度運動を続けるのです。
というわけで答えは ④ です。