断熱材で囲まれた図3のような容器に、20℃ の水 200g が入っている。この水の中に 65℃ に温められた 500g の金属球を入れて、かくはん棒で静かにかき混ぜ続けた。しばらくすると水温は 30℃ で一定になった。ただし、水と金属球以外の熱容量は無視できるとする。
（問6）金属球の比熱はいくらか。ただし、水の比熱を 4.2 J/(g⋅K) とする。
（問7）金属球を水に入れた瞬間から熱平衡になるまでの、金属球と水の温度変化を表す図として最も適当なものを、次の①～⑥のうちから一つ選べ。ただし、金属球の温度は一様とする。
#センター08追試
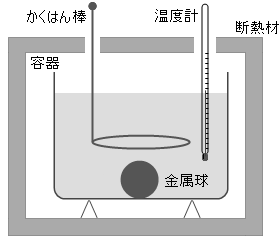
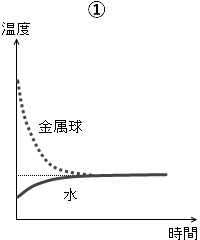
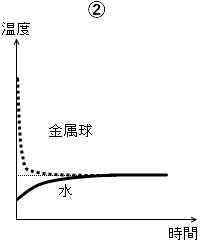
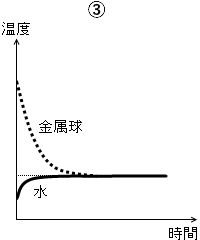
（問6）
求める比熱を c とします。
水が得た熱量（ Q = mcΔT ）は
200 × 4.2 × (30 - 20)
金属球が失った熱量は
500 × c × (65 - 30)
熱量保存則より、
200 × 4.2 × (30 - 20) = 500 × c × (65 - 30)
∴ 200 × 4.2 × 10 = 500 × c × 35
∴ 2 × 4.2 × 10 = 5 × c × 35
∴ 2 × 4.2 × 2 = 1 × c × 35
∴ 4.2 × 4 = c × 35
∴ c = \(\large{\frac{16.8}{35}}\) = \(\large{\frac{33.6}{70}}\) = 0.48 [J/(g⋅K)]
（問7）
問題文中の「ただし、金属球の温度は一様とする。」という意味は、金属球の内部と表面部分で温度が同じという意味です。
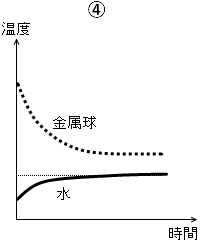
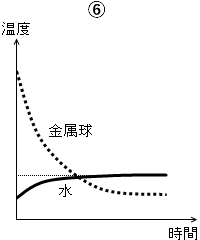
熱平衡になったというのだから温度が同じにならなければおかしいので、④、⑥は除外できます。
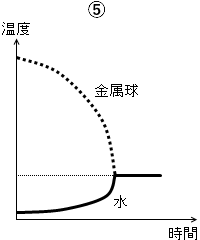
温度差が大きいときほど熱平衡に向かうスピードは速く、温度が近くなってくるほどゆっくり熱平衡に向かうだろうから⑤も除外できます。（ジュースを急いで冷やしたいときに、冷蔵庫より冷凍庫に入れた方が早いことと同じ。）
そして、金属球と水は同時に熱平衡温度に達するはずです。どちらかが先に熱平衡温度に達するというのはおかしいです。
答えは ① です。
（もう少し厳密に説明しますと）
金属球における熱平衡温度との温度差を ΔT金 、水における熱平衡温度との温度差を ΔT水 としますと、熱量保存則より、
500 × 0.48 × ΔT金 = 200 × 4.2 × ΔT水
∴ \(\large{\frac{ΔT_金}{ΔT_水}}\) = \(\large{\frac{200×4.2}{500×0.48}}\) = \(\large{\frac{2×4.2}{5×0.48}}\) = \(\large{\frac{2.1}{5×0.12}}\) = \(\large{\frac{0.7}{5×0.04}}\) = \(\large{\frac{7}{2}}\)
であり、
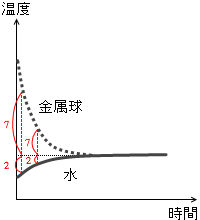
となっています。