次の文章中の空欄ア・イに入れる数値と記号の組合せとして最も適当なものを、下の①～⑥のうちから一つ選べ。
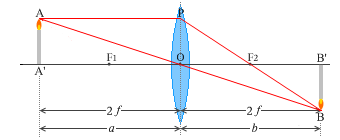
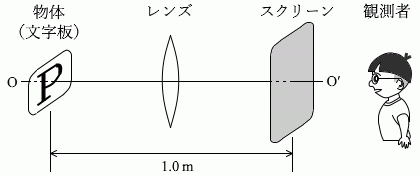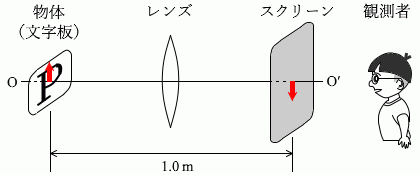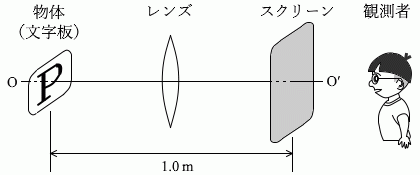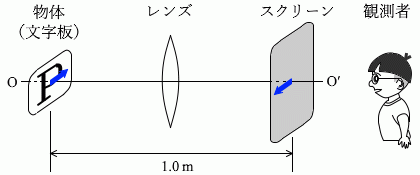
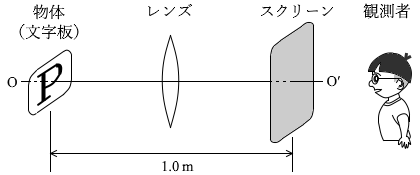
図2のように、直線OO'に垂直に、物体（文字板）と半透明のスクリーンを 1.0m 離して設置した。凸レンズの光軸を直線OO'と一致させたまま、物体とスクリーンの間でレンズの位置を調整したところ、スクリーン上に倍率 1.0 の明瞭な像ができた。このことから、レンズの焦点距離はアm であることがわかる。また、スクリーン上の像をO'側から観察すると、図3のイのように見える。
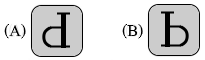
| ア | イ | |
|---|---|---|
| ① | 0.25 | (A) |
| ② | 0.25 | (B) |
| ③ | 0.50 | (A) |
| ④ | 0.50 | (B) |
| ⑤ | 1.0 | (A) |
| ⑥ | 1.0 | (B) |
#センター19本試物理
ア
倍率 1.0 の像ができたということだから、これは『凸レンズ』項における \(m\) の値が 1.0 ということであり、レンズの公式（写像公式）
\({\large\frac{1}{a}} + {\large\frac{1}{b}} = {\large\frac{1}{f}}\)
において \(a = b\) ということであり、これはつまり
\({\large\frac{1}{a}} + {\large\frac{1}{a}} = {\large\frac{1}{f}}\)
ということであり、これを計算すると \(a = 2f\) になり、結局レンズの公式は
\({\large\frac{1}{2f}} + {\large\frac{1}{2f}} = {\large\frac{1}{f}}\)
と表されることになり、これは『凸レンズ』項の『\(a = b\) すなわち \(m = 1\) のとき』に相当し、ろうそくのイラストで表現すると、
となり、このイラストの \(4f\) が本問では 1.0m であるので、レンズの焦点距離（\(f\)）は 0.25m ということになります。
イ
上記イラストで示したようにスクリーンに映る像は反転するわけですが、これは上下方向だけでなく左右方向についてもです（レンズは円いので）。
上下、左右ともに反転している像は(A)、(B)のうちの (A) です。
というわけで答えは ① です。