平行な電流の間にはたらく力
平行な電流の間には力がはたらく
平行な導線に電流を流すと、片方の電流がつくる磁場によってもう片方の電流が力を受け、導線同士が引き合ったり反発し合ったりします。
導線Bが受ける力
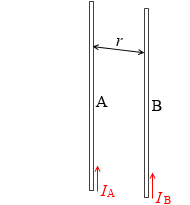 左図のように、距離 r [m] だけ離れた2本の平行な長い導線A、Bにそれぞれ IA [A] 、IB [A] の電流が、同じ向きに流れているとします。
左図のように、距離 r [m] だけ離れた2本の平行な長い導線A、Bにそれぞれ IA [A] 、IB [A] の電流が、同じ向きに流れているとします。
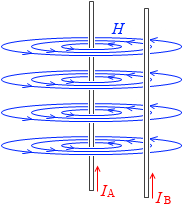 導線Aがつくる磁場は、
導線Aがつくる磁場は、
H = \(\large{\frac{I_\rm A}{2\pi r}}\) ……①
であり、
導線Bのうち、長さ l の部分が、この磁場から受ける力は、
F = μ0IBHlsinθ (今、空気中での話であるとして透磁率は μ0 とします。)
ですが、
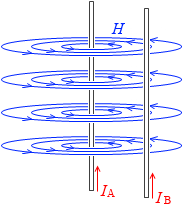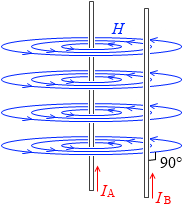 今、2つの導線は平行であり、導線Aがつくる磁場と導線Bの角度は垂直です。sinθ = sin90° = 1 です。
今、2つの導線は平行であり、導線Aがつくる磁場と導線Bの角度は垂直です。sinθ = sin90° = 1 です。
つまり、
F = μ0IBHl
です。この式の H のところに①式を代入すると、
F = μ0IB\(\large{\frac{I_\rm A}{2\pi r}}\)l
= \(\large{\frac{μ_0I_{\rm A}I_\rm{B}}{2\pi r}}\)l
となり、これが導線Bが受ける力の大きさになります。この式は l [m] の導線部分に加わる力の大きさのことですが、もし 1m 当たりに加わる力を求めるとすると、l = 1 とし、
F = \(\large{\frac{μ_0I_{\rm A}I_\rm{B}}{2\pi r}}\)
となります。
導線Aが受ける力
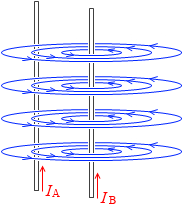 上とまったく同じように考えていくと、導線Aが受ける力は、
上とまったく同じように考えていくと、導線Aが受ける力は、
F = \(\large{\frac{μ_0I_{\rm A}I_\rm{B}}{2\pi r}}\)l
となり、これはつまり導線Aが受ける力は導線Bが受ける力とまったく同じになるということです。これは当たり前です。作用⋅反作用の法則です*力学における作用⋅反作用はイメージしやすいですが、電磁気学における作用⋅反作用はイメージしにくいかもしれません。
でもこれは作用⋅反作用の法則の一種です。
閉じる
。
平行な電流の間にはたらく力
結局、平行な電流の間にはたらく力というのは、
F = \(\large{\frac{μ_0I_{\rm A}I_\rm{B}}{2\pi r}}\)l
です。
( 導線Bが受ける力と導線Aが受ける力を足して、
F = 2\(\large{\frac{μ_0I_{\rm A}I_\rm{B}}{2\pi r}}\)l
になる、なんて考えてはだめです。)
力の向き
力の向きについては、フレミングの左手の法則により、下図のようになります。左手を使ってよく考えてみてください。右ねじの法則も思い出してください。
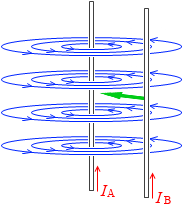 導線Bが受ける力
導線Bが受ける力 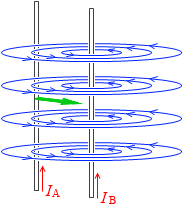 導線Aが受ける力
導線Aが受ける力
つまり、同じ向きの平行な電流は引き合うのです。
逆に、反対向きの平行な電流は反発し合います。下図のようになります。
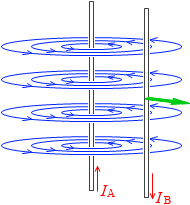 導線Bが受ける力
導線Bが受ける力  導線Aが受ける力
導線Aが受ける力
このことは、しばしば以下のように説明されます。(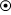 は紙面の向こう側からこちら側へ、
は紙面の向こう側からこちら側へ、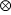 は紙面こちら側から向こう側へ、電流が流れているということを示しています。)
は紙面こちら側から向こう側へ、電流が流れているということを示しています。)
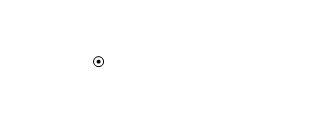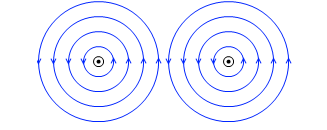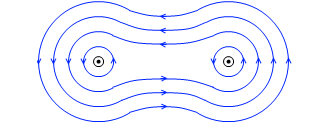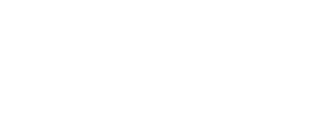 電流が同じ向きの場合、
電流が同じ向きの場合、
2つの導線の間の部分の磁場は向きが違うので弱め合い、磁力線の密度が少なくなり、それを解消しようと導線が近づこうとする。
 電流の向きが反対の場合、
電流の向きが反対の場合、
2つの導線の間の部分の磁場は向きが同じなので強め合い、磁力線の密度が多くなり、それを解消しようと導線は離れようとする。
このように、電流が流れる導線は、磁力線の”粗密”が解消されるような方向に動く、という法則があります。このことは覚えておくと何かと便利です。