非線形抵抗
線形と非線形
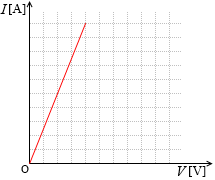 オームの法則 V = RI をグラフで表すと右図のようになります。これは、抵抗に電圧を掛けると電圧に比例して電流が大きくなる、ということを示しています。
オームの法則 V = RI をグラフで表すと右図のようになります。これは、抵抗に電圧を掛けると電圧に比例して電流が大きくなる、ということを示しています。
しかし厳密には、抵抗というものは電流が大きくなるにつれてジュール熱で温度が上がり抵抗率が大きくなってしまいます。抵抗の値が大きくなってしまうのです。
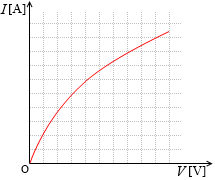 電圧を上げて電流を大きくしていくと抵抗が大きくなっていく、ということをグラフで表すと右図のようになります。電圧を上げていっても思うように電流が大きくなってくれません。
電圧を上げて電流を大きくしていくと抵抗が大きくなっていく、ということをグラフで表すと右図のようになります。電圧を上げていっても思うように電流が大きくなってくれません。
数学や物理では、「比例」していることを「線形」といい、「比例していない」場合を「非線形」といいます。
『抵抗率の温度変化』の表で、物質別の抵抗率の温度係数を紹介しましたが、
ニクロムという物質は温度係数がとても小さく、電流が大きくなっても抵抗の値があまり変わりません。オームの法則 V = RI が比較的きれいに成り立ち、グラフの曲線が真っ直ぐです。(狭い範囲では)「線形」の特性を持つ素材とみなせます。
一方、タングステンという物質は(白熱電球のフィラメントに使われる素材ですが)、温度係数が大きく、電流が大きくなると温度が上がり抵抗が大きくなってしまいます。V = RI は成り立たずグラフの曲線は曲がったものになってしまいます。「非線形」の特性を持つ素材です。このような素材でできた抵抗を非線形抵抗(あるいは非オーム抵抗)といいます。
線形の抵抗
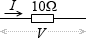
 線形の特性を持つ素材で 10Ω の抵抗があるとします。この抵抗に V [V] の電圧を掛けたときの電流を I [A] とすると、
線形の特性を持つ素材で 10Ω の抵抗があるとします。この抵抗に V [V] の電圧を掛けたときの電流を I [A] とすると、
V = 10I ……①
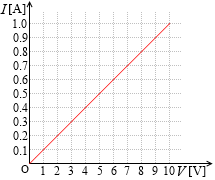
という式が立てられ、この式を表すグラフは右図のようになります。
この抵抗に 8.0Ω の抵抗と 8.0V の起電力を直列に接続したとします。
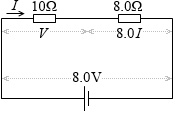
 すると、
すると、
8.0V = V + 8.0Ω×I ……②
∴ 8.0I = 8.0 - V
∴ I = 1.0 - \(\large{\frac{V}{8.0}}\) ( I 切片が 1.0 、V 切片が 8.0 )
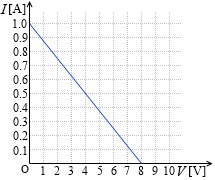
という式が立てられ、この式を表すグラフは右図のようになります。
10Ω の抵抗に流れる電流 I (回路に流れる電流のことでもあります)を求めてみます。①式を②式に代入して、
8.0 = 10I + 8.0I
 ∴ 18I = 8.0
∴ 18I = 8.0
∴ I = \(\large{\frac{4}{9}}\) ≒ 0.44
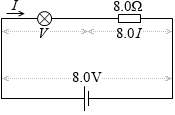
2つの式を使って電流の値を求めることができました。
この値は2つのグラフの曲線の交点のことでもあります。
非線形の抵抗
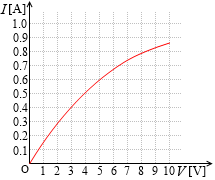 非線形の特性を持つ抵抗(たとえば電球
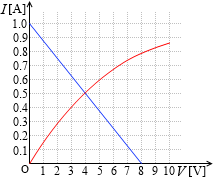
非線形の特性を持つ抵抗(たとえば電球 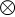 )があるとします。この抵抗に V [V] の電圧を掛けたときの電流 I [A] の値は数式で表すことができず、実験値から右図のグラフが得られたとします。
)があるとします。この抵抗に V [V] の電圧を掛けたときの電流 I [A] の値は数式で表すことができず、実験値から右図のグラフが得られたとします。
上と同じように、この抵抗に 8.0Ω の抵抗と 8.0V の起電力を直列に接続したとします。
 すると上の線形の抵抗の場合のときと同じように、
すると上の線形の抵抗の場合のときと同じように、
8.0V = V + 8.0Ω×I ……②
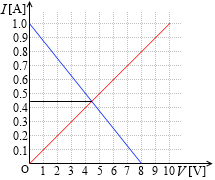
という式が立てられ、この式を表すグラフは右図のようになります。
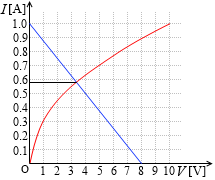
そして同じように電流 I を求めようとすると、今度は式が1つしかないので方程式が解けません。こういうときは数式で解くのをあきらめてグラフを使って値を求めます。
 2つのグラフの曲線を重ね合わせたときの交点が求める解です。グラフの目盛りを読み取ります。右図の目盛りを読み取ると電流 I は 0.50A です。
2つのグラフの曲線を重ね合わせたときの交点が求める解です。グラフの目盛りを読み取ります。右図の目盛りを読み取ると電流 I は 0.50A です。
念のため、おことわり
ここまでの説明を読んで「非線形のときは必ずグラフを使って解く」と思われたかもしれませんが、非線形のときであってもグラフを使わず数式で解ける場合も無くは無いです。
 非線形の特性を持つ抵抗がたまたま
非線形の特性を持つ抵抗がたまたま
V = 10I2 ……③
というきれいな式を満たす場合、上の例で挙げた回路に接続すると、
8.0V = V + 8.0Ω×I ……②
という式も満たすことになり、③式を②式に代入して解いていくと、
8.0 = 10I2 + 8.0I
10I2 + 8.0I = 8.0
I2 + \(\large{\frac{8}{10}}\)I = \(\large{\frac{8}{10}}\)
I2 + \(\large{\frac{4}{5}}\)I = \(\large{\frac{4}{5}}\) (平方完成の形に持っていくと)
I2 + 2\(\large{\frac{2}{5}}\)I + \(\large{\frac{2^2}{5^2}}\) = \(\large{\frac{4}{5}}\) + \(\large{\frac{2^2}{5^2}}\)
(I + \(\large{\frac{2}{5}}\))2 = \(\large{\frac{20}{25}}\) + \(\large{\frac{4}{25}}\)
(I + \(\large{\frac{2}{5}}\))2 = \(\large{\frac{24}{25}}\)
I + \(\large{\frac{2}{5}}\) = \(\sqrt{\large{\frac{24}{25}}}\) (∵ I > 0)
I + \(\large{\frac{2}{5}}\) = \(\sqrt{\large{\frac{4\times 6}{25}}}\)
I = \(\large{\frac{2}{5}}\small{\sqrt{6}}\) - \(\large{\frac{2}{5}}\)
I = \(\large{\frac{2}{5}}\)(\(\small{\sqrt{6}}\) - 1) ≒ \(\large{\frac{2}{5}}\)(2.449 - 1) = \(\large{\frac{2}{5}}\)×1.449 ≒ 0.58
 と求められます。
と求められます。
この値はグラフからも読み取れます。