コンデンサーを含む直流回路
直流回路におけるコンデンサーの充電、放電
コンデンサーを電池につないだときの様子については『コンデンサーの接続』項である程度説明しましたが、本項ではスイッチや抵抗と一緒につないだときのコンデンサーの充電、放電の様子について説明します。
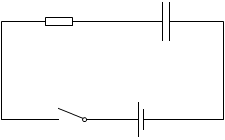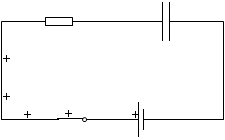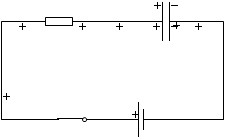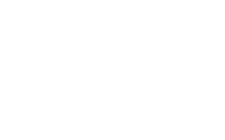
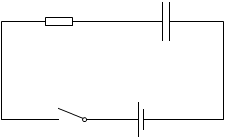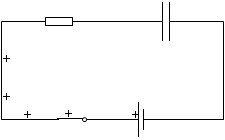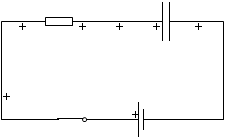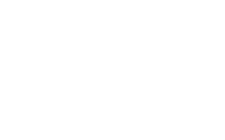
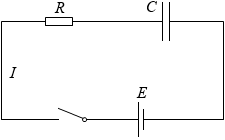 C [F] の電気容量のコンデンサーと、R [Ω] の抵抗と、E [V] の起電力で内部抵抗が無い電池と、さらにスイッチを直列につないだ回路を考えます。コンデンサーの両端の電圧を V [V] 、コンデンサーの電荷(電気量)を Q [C] 、回路を流れる電流を I [A] とします。
C [F] の電気容量のコンデンサーと、R [Ω] の抵抗と、E [V] の起電力で内部抵抗が無い電池と、さらにスイッチを直列につないだ回路を考えます。コンデンサーの両端の電圧を V [V] 、コンデンサーの電荷(電気量)を Q [C] 、回路を流れる電流を I [A] とします。
コンデンサーの充電
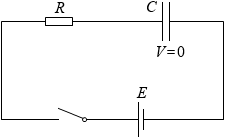 スイッチを閉じる前はコンデンサーには電荷がまったく溜まってないので V = 0 です。
スイッチを閉じる前はコンデンサーには電荷がまったく溜まってないので V = 0 です。
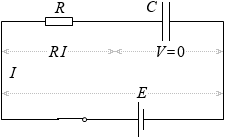 スイッチを閉じた瞬間は、起電力の電圧がすべて抵抗の部分に掛かるので E = RI、つまり電流は、
スイッチを閉じた瞬間は、起電力の電圧がすべて抵抗の部分に掛かるので E = RI、つまり電流は、
I = \(\large{\frac{E}{R}}\)
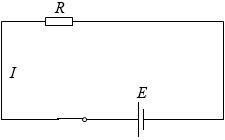 です。これは、まるでコンデンサーが無いかのように電流が流れるということです。
です。これは、まるでコンデンサーが無いかのように電流が流れるということです。
 電荷が溜まってない空のコンデンサーに電圧を掛けると電荷が次々に溜まっていきますが、
電荷が溜まってない空のコンデンサーに電圧を掛けると電荷が次々に溜まっていきますが、
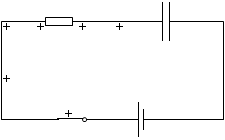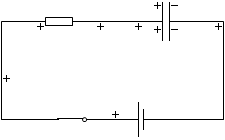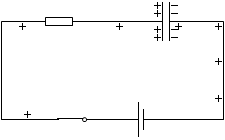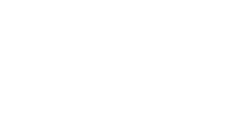 (スローモーション)
(スローモーション)
 その様子は、まるでコンデンサーが存在していないかのようです。
その様子は、まるでコンデンサーが存在していないかのようです。
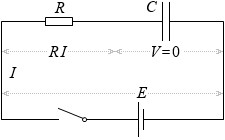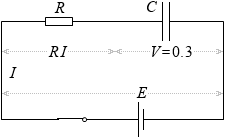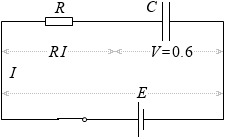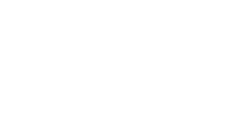 しかし、コンデンサーに電荷が溜まるにつれて極板間に電位差ができてきます。
しかし、コンデンサーに電荷が溜まるにつれて極板間に電位差ができてきます。
このときの電圧の関係式(キルヒホッフの第2法則の式)は、
E = RI + V
∴ I = \(\large{\frac{E-V}{R}}\)
となります。
上の方で示したスイッチを閉じた瞬間の電流の式 I = \(\large{\frac{E}{R}}\) は、上式の右辺の V が 0 の場合である、とみなせます。V が大きくなっていくと I が小さくなっていきます。コンデンサーに電荷が溜まっていき、V が大きくなっていくと、電流 I が小さくなるということです。E = RI + V の式でいえば V が大きくなると RI が小さくなるということです。
だんだん V が大きくなっていって E と同じ大きさになると電流は流れなくなります。I = \(\large{\frac{E-V}{R}}\) の式において右辺の分子が E - E になるということです。E = RI + V の式でいえば、右辺第一項の RI が 0 になるということです。抵抗 R には電流も流れてないし電圧も掛かってないという状態です。
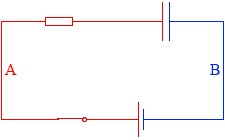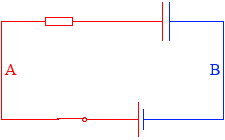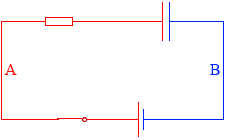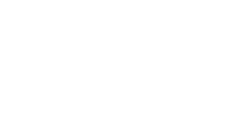 『コンデンサーの接続』項で説明したように、左図のAの領域が等電位、Bの領域が等電位になったところでコンデンサーの充電は終わります。
『コンデンサーの接続』項で説明したように、左図のAの領域が等電位、Bの領域が等電位になったところでコンデンサーの充電は終わります。
Aの領域とBの領域の電位差は E です。
電流が流れなくなったという状態は、電荷同士の押し合いへし合いが止まった、という状態です。
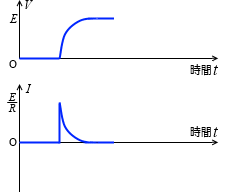 ここまでの現象の電圧と電流についてのグラフを描くと、左図のようになります。
ここまでの現象の電圧と電流についてのグラフを描くと、左図のようになります。
スイッチを閉じた瞬間はまるでコンデンサーが存在しないかのように電流が流れ、コンデンサーの電圧 V が起電力 E に等しくなると電流は止まります。
このコンデンサーの充電は実際にはごく短時間で終了します。
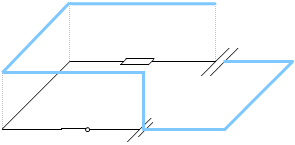 コンデンサーの充電が終わったあとのこの電気回路の電位差のイメージ図を描くと、左図のようになります。『キルヒホッフの法則』項の『電位差のイメージ図』では抵抗の部分が坂道になっていましたが、今回は違います。抵抗というものは電流が流れているときだけ電圧降下が起こります。充電が終わったあとのこの回路では電流が流れてないので電圧降下は起こりません。コンデンサーの充電が終わると今度は抵抗が存在しないかのような状態になります。
コンデンサーの充電が終わったあとのこの電気回路の電位差のイメージ図を描くと、左図のようになります。『キルヒホッフの法則』項の『電位差のイメージ図』では抵抗の部分が坂道になっていましたが、今回は違います。抵抗というものは電流が流れているときだけ電圧降下が起こります。充電が終わったあとのこの回路では電流が流れてないので電圧降下は起こりません。コンデンサーの充電が終わると今度は抵抗が存在しないかのような状態になります。
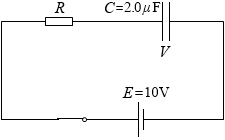 充電が終わったコンデンサーの電荷(電気量)は Q = CV です。
充電が終わったコンデンサーの電荷(電気量)は Q = CV です。
たとえば、この回路の起電力 E が 10V で、電気容量 C が 2.0μF であった場合、
コンデンサーの電圧 V は E と同じなので、
コンデンサーに溜められた電荷は Q = CV = 2.0μF×10V = 20μC です。
電池と導線を入れ替え
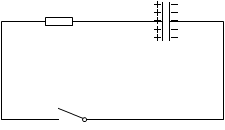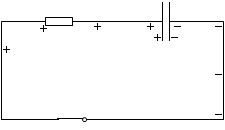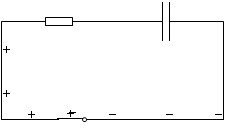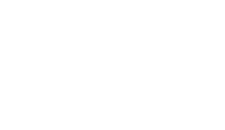
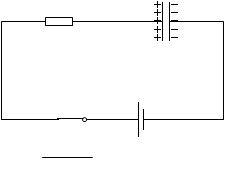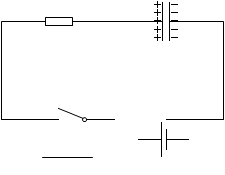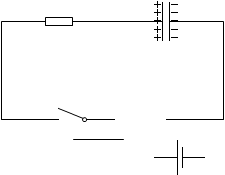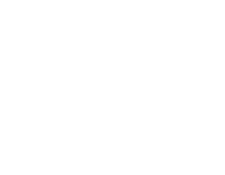 次に、スイッチを開いて、電池を外して、導線と入れ替えてみます。
次に、スイッチを開いて、電池を外して、導線と入れ替えてみます。
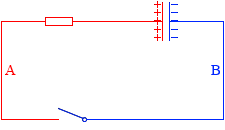 この状態では、Aの領域が等電位で、Bの領域が等電位です。
この状態では、Aの領域が等電位で、Bの領域が等電位です。
図では、+ の電荷や - の電荷は極板上にだけ描かれてますが、実際には、Aの領域全体に + の電荷が存在していてそれぞれが押し合いへし合いをしてつり合った状態で静止しています。- の電荷についても同様です。
コンデンサーの放電
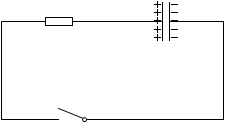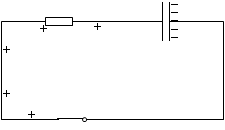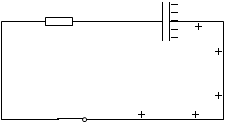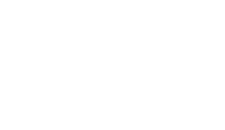
 次に、再びスイッチを閉じます。
次に、再びスイッチを閉じます。
すると、極板間にいた電荷たちが動き出し、+ の電荷と - の電荷が中和し、全体が等電位になります。
コンデンサーの放電です。
このときの電流の向きは、充電のときと逆です。量記号で書くと - I と表せます。
 B領域の - 電荷についてですが、- 電荷が動くときそれは + 電荷が逆向きに動くことと同等です。ですから上図は左図のように描き直すこともできます。
B領域の - 電荷についてですが、- 電荷が動くときそれは + 電荷が逆向きに動くことと同等です。ですから上図は左図のように描き直すこともできます。
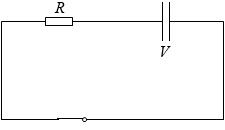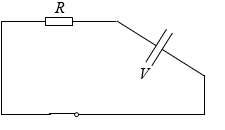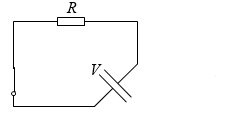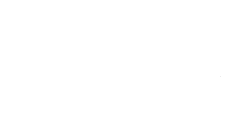
 R の抵抗に掛かかる電圧は V です。
R の抵抗に掛かかる電圧は V です。
ですのでオームの法則の式は、
V = R × (- I )
であり、電流の大きさは、
I = - \(\large{\frac{V}{R}}\)
です。スイッチを閉じた瞬間については V = E ですので、
I = - \(\large{\frac{E}{R}}\)
です。
 + の電荷と - の電荷が次々に中和していくと、コンデンサーの電圧は下がり、上式の V は小さくなっていきます。I も徐々に 0 になっていきます。
+ の電荷と - の電荷が次々に中和していくと、コンデンサーの電圧は下がり、上式の V は小さくなっていきます。I も徐々に 0 になっていきます。
徐々にといっても実際にはコンデンサーの放電はごく短時間で終了します。
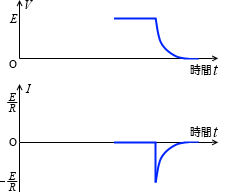 この放電に関する電圧と電流についてのグラフを描くと、左図のようになります。
この放電に関する電圧と電流についてのグラフを描くと、左図のようになります。
コンデンサーの充電、放電のグラフ
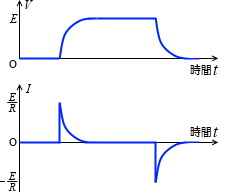 充電と放電のグラフを合わせて描くと、左図のようになります。
充電と放電のグラフを合わせて描くと、左図のようになります。
2つの視点
『静と動』で説明したように、電気には大きく分けて静電気と動電気(電流が流れている状態)がありますが、コンデンサーを含む電気回路について考えるときは、静電気的視点と動電気的視点の両方が必要です。