ローレンツ力

ローレンツ力

電荷を持つ粒子、荷電粒子が磁場の中で運動すると力を受けます。ローレンツ力といいます＊ろーれんつりょく。
19世紀のオランダの物理学者 ヘンドリック・ローレンツ Hendrik Lorentz にちなんでいます。
　閉じる。陰極線に磁場を掛けたときにその軌道が曲がる原因になる力です。荷電粒子は磁場を横切るとき必ずローレンツ力を受けます。

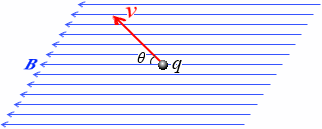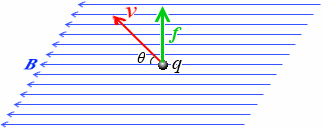磁束密度 B [T] の磁場の中を電気量 q [C] の荷電粒子が速度 v [m/s] で進んでいて、磁場の方向と速度の方向のなす角が θ であるとします。

この荷電粒子は磁場の方向と速度の方向の両方に垂直な方向に力を受けます。この力を f [N] で表すと次のようになります。

ローレンツ力は電気量、速度、磁束密度に比例します。sinθ は、磁場の方向と速度の方向が直角に近いほど力が大きくなる、という意味です。『電流が磁場から受ける力』を参照してください。

ローレンツ力＝電流が磁場から受ける力

実は、ローレンツ力

　　　　f = qvBsinθ

は、電流が磁場から受ける力

　　　　F = IBlsinθ

と同等のものです。

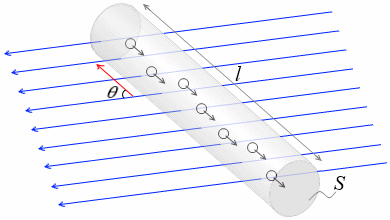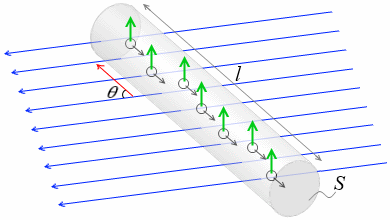磁束密度 B [T] の磁場の中に長さ l [m] 、断面積 S [m²] の導線があるとします。流れている電流を I [A] 、自由電子の電荷を -e [C] 、自由電子の平均速度を v [m/s] 、導線内に存在する自由電子の数密度を n [個/m³] 、磁場の方向と導線の方向のなす角を θ とします。

自由電子1個にはたらくローレンツ力は、q のところに -e を代入して、

　　　　f = -evBsinθ

です。この力の向きについては後で考えるとして、力の大きさだけでいえば、

　　　　f = evBsinθ

です。

次に、この導線の中に自由電子がいくつあるか考えてみますと、それは、

　　　　nSl 個

です＊導線の体積（断面積×長さ）は S×l [m³] です。いま数密度が n [個/m³] なのだから、この導線内に存在する自由電子の総数は n×Sl 個です。
もしたとえば、数密度が 300個/m³で、断面積が 2m² で、長さが 10m だったら、総数は 6000個です。
　閉じる。ですので、この導線内の自由電子すべてに掛かるローレンツ力を総合すると、

　　　　f × nSl

　　　　= evBsinθ × nSl

　　　　= envSBlsinθ

です。そして電流というのは I = envS です。これを上式に代入すると、

　　　　F = IBlsinθ

となり、これは「電流が磁場から受ける力」のことです。

ローレンツ力の向き

上で、ローレンツ力は磁場の方向と速度の方向の両方に垂直な方向、といいましたが、この方向というのはフレミングの左手の法則にのっとった方向です。

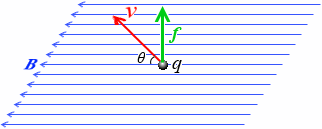ただし、これは q が正のときの話です。

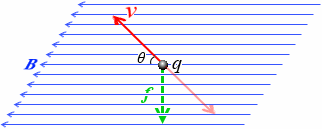もし q が負ならば左図のような方向です。v の向きを逆向きにしてからフレミングの左手の法則を適用しなければなりません。

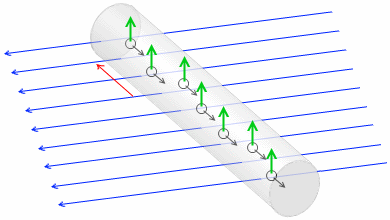上で、自由電子1個にはたらくローレンツ力は f = -evBsinθ といいましたが、これも q が負のパターンです。v の向きと逆の向きを仮定してフレミングの左手の法則を適用して力の向きを求めなければなりません。といいますか、v の逆向きというのは電流の向きのことです。

フレミングの左手の法則は「電子」ではなく「電流」の向きを当てはめる法則です。