人工衛星

人工衛星の速さ

地球を周回する人工衛星は、地球と人工衛星の間にはたらく万有引力を向心力として、地球の周りを回っています。人工衛星自体に推進力があるわけではありません＊全く無いわけではないでしょうが、推進装置が付いていたとしてもそれは姿勢を変えるためだけの微々たる推進力しかなく、人工衛星を加速したり減速したりするほどの力は無いと思います。
　閉じる。

つまりこれは、糸の先に付けられた物体がくるくると回されているような状態です。

このときの糸の張力が、万有引力に当たります。

この人工衛星の速さについて考えてみます。

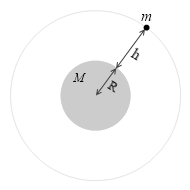質量 m の人工衛星が、地表から h の高さを等速円運動しているとします。地球の質量を M 、地球の半径を R 、重力加速度の大きさを g 、万有引力定数を G とし、人工衛星の速さ v を求めます。

まずこの円運動の運動方程式を立てます。運動方程式を立てるということは　ma = F　の式を立てるということであり、

つまり立てたい運動方程式は以下のようになります。

　　　　m\(\large{\frac{v^2}{R+h}}\) = G\(\large{\frac{Mm}{(R+h)^2}}\)

　　∴　　　v² = G\(\large{\frac{M}{R+h}}\)

　　∴　　　v = \(\sqrt{\large{\frac{GM}{R+h}}}\)

GM = gR² を代入して別の形で表現すれば、

　　　　　v = \(\sqrt{\large{\frac{gR^2}{R+h}}}\)

となります。

この式を吟味してみますと、G も、M も、g も、R も、すべて定数でありますから、この v の式というのは h のみで決まるということになります。人工衛星の質量 m も関係ありません。質量が大きく万有引力が大きくても、その分、動きにくいのでトータルで相殺されます。つまり人工衛星の速さというものは、地表からの高さのみで決まり、高いところにあるものほど速さが遅い、といえます。

第1宇宙速度

地表で水平方向に大砲を撃つと、砲弾はある程度の距離を飛んで地面に墜落します。このとき大砲の威力が大きければ、つまり砲弾の初速度が大きければ、その分、飛距離は伸びます。どんどん初速度を大きくしていくと、やがて砲弾は地球を一周します。実際には起こり得ない仮定ではありますが、空気抵抗が無く、砲弾の初速をいくらでも大きくできると仮定した場合、どれくらいの初速を与えると地球を一周するか考えてみます。

今、空気抵抗が無いと仮定したので、砲弾は減速しません。つまり地球を一周する場合は、初速を保ったまま一周するわけです。これはつまり等速円運動です。そして地表すれすれを飛ぶとすると、この円運動の半径は地球の半径 R ということになります。

砲弾の質量を m とすると、砲弾には mg の重力が掛かり、これが円運動の向心力です。

求める速さを v とすると、この円運動の運動方程式は、

　　　　m\(\large{\frac{v^2}{R}}\) = mg

となりますので、求める速さは

　　　　v² = gR

　∴　　v = \(\sqrt{gR}\)

となります。これは上で求めた人工衛星の速さの式　v = \(\sqrt{\large{\frac{gR^2}{R+h}}}\)　に h=0 を代入しても求められます。

この速度を第1宇宙速度といいます。推進力を持たない物体が地表すれすれを飛び続けるための速度です。（地表すれすれでなく、ある程度の高度で地球を一周する場合は、上の人工衛星の速さの式の h が 0 でなくなり、必要な速度 v はもっと小さくなります。下で説明する第2宇宙速度においても同じようなことがいえます。）

重力加速度 g = 9.8 m/s² 、地球の半径 R = 6.4×10⁶ m として第1宇宙速度の具体的な数値を求めてみますと、

　　　　v = \(\sqrt{gR}\)
　　　　　= \(\sqrt{\small{9.8\times6.4\times10^6}}\)
　　　　　= \(\sqrt{\small{49\times2\times10^{-1}\times64\times10^{-1}\times10^6}}\)
　　　　　= \(\sqrt{\small{7^2\times2\times8^2\times10^{-1}\times10^{-1}\times10^6}}\)
　　　　　= \(\sqrt{\small{7^2\times2\times8^2\times10^4}}\)
　　　　　= 7×8×10²×\(\sqrt{2}\)
　　　　　≒ 56×10²×1.41
　　　　　≒ 79.0×10²
　　　　　= 7.9×10³

第1宇宙速度は 約7.9×10³m/s つまり 約7.9km/s です。

地球に大気が無くて空気抵抗が無い場合、この速さで水平向きに大砲を撃てば砲弾は地球を一周して戻ってくるということです。地球一周は 約4万km ですからこれを 7.9 で割ると 約5000秒 ≒ 約1.4時間です。このくらいの時間で地球を一周するような速さということです。

静止衛星

日々の天気予報の衛星画像は気象衛星ひまわりが撮影したものですが、この気象衛星が常に日本を撮影しているということは、この人工衛星は日本の上空に静止しているということです。このような人工衛星を静止衛星といいます。これは宇宙からみれば、人工衛星が日本と一緒に回転しているということです。

静止衛星の軌道

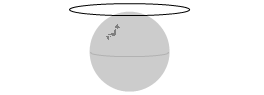しかし人工衛星は左図のような軌道はとれません。

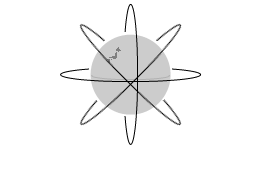円軌道の中心は地球の中心でなければなりません。

人工衛星が地球の周りを回るのは、万有引力によって引きつけ合っていて、それが向心力となって円運動しているのです。万有引力は物体の中心と物体の中心を結んだ方向＊厳密にいえば、物体の「重心」と物体の「重心」
　閉じるにはたらくものですから、人工衛星の軌道は必ず左図のようになります。上図では軌道の中心が北極付近になってしまっています。これでは万有引力ではありません。

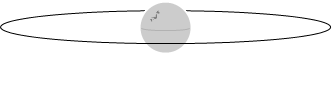
そしてこれらの軌道のうち、日本に追随して回転できるのは赤道上空の軌道だけです。

赤道上空の軌道というのは左図のような軌道です。

静止衛星の高さ

さらに、日本と一緒に回転するためには回転速度（= 角速度）が地球の自転と同じでなければなりません。つまり24時間で一回転しなければなりません。

上の『人工衛星の速さ』のところで説明しましたが、人工衛星の速さは高さによります。低い位置にある人工衛星は速く、高い位置にある人工衛星は遅いです。これはつまり、24時間で一周するような速さというのはその高さが決まっているということです。

この高さを求めてみます。

まず、人工衛星の運動方程式から角速度の式を導き出してみます。

上の『人工衛星の速さ』のところで示した運動方程式は、

　　　　m\(\large{\frac{v^2}{R+h}}\) = G\(\large{\frac{Mm}{(R+h)^2}}\)

でしたが、分かりやすくするため、R+h を r とおきます。つまり人工衛星の高さを地球の中心からの距離 r とおきます。すると、

　　　　m\(\large{\frac{v^2}{r}}\) = G\(\large{\frac{Mm}{r^2}}\)

となります。次に左辺の v に v = rω を代入します。すると、

　　　　mrω² = G\(\large{\frac{Mm}{r^2}}\)

　　∴　　ω² = G\(\large{\frac{M}{r^3}}\)　　……①

となります。この角速度 ω が、24時間で一周となればいいわけです。

24時間で一周という角速度は

　　　　ω = \(\large{\frac{2\pi}{T}}\) = \(\large{\frac{2\pi\ \rm{rad}}{24\ \rm{h}}}\) ≒ \(\large{\frac{2\times3.14\ \rm{rad}}{24\times60\times60\ \rm{s}}}\) = \(\large{\frac{3.14}{12\times60\times60}}\) [rad/s]

この値と、万有引力定数 G = 6.67×10^-11 と、地球の質量 M = 6.0×10²⁴ kg を ①式に代入して静止衛星の高さ r を求めます。

　　　　ω² = G\(\large{\frac{M}{r^3}}\)

　⇒　　\(\Bigl(\large{\frac{3.14}{12\times60\times60}}\bigr)\small{^2}\) = \(\large{\frac{6.67\times10^{-11}\times6.0\times10^{24}}{r^3}}\)

　∴　　r³ = \(\large{\frac{(12\times60\times60)^2\times6.67\times10^{-11}\times6.0\times10^{24}}{3.14^2}}\)

　　　　　= \(\large{\frac{12^2\times6^2\times6^2\times10^4\times6.67\times10^{-11}\times6.0\times10^{24}}{3.14^2}}\)

　　　　　= \(\large{\frac{12^2\times6^2\times6^2\times6.67\times6.0\times10^{17}}{3.14^2}}\)

　　　　　≒ 757500×10¹⁷

　　　　　= 75.75×10²¹

　∴　　r ≒ \(\sqrt[3]{75.75}\)×10⁷

　　　　　≒ 4.23×10⁷

というわけで、静止衛星は地球の中心から 約4.23×10⁷m （約42300km）の高さにある、と分かりました。

この高さは地球の半径 R ≒ 6.4×10⁶ m と比べますと、

　　\(\large{\frac{r}{R}}\) = \(\large{\frac{4.23\times10^7}{6.4\times10^6}}\) ≒ 6.6

約6.6倍の高さと分かります。

地表からの高さでいえば　4.23×10⁷ - 6.4×10⁶ = 3.59×10⁷ m、約3万6000km です。＊ちなみにエベレストの高さは約8kmです。
　閉じる

この赤道上空高度 約3万6000km の円軌道を静止軌道といいます。

人工衛星でなくても、たとえば石ころでも、この位置にいれば地球と一緒に回転するということです。

この静止軌道は世界各国から打ち上げられた気象衛星、通信衛星、放送衛星などの静止衛星がひしめき合っています。＊もちろん、静止軌道を通らない（=静止衛星でない）人工衛星もたくさんあります。
　閉じる

第2宇宙速度

上の『第1宇宙速度』のところで、地表から水平に 約7.9km/s で大砲を撃つと砲弾は地球を一周して戻ってくるという話をしましたが、このとき初速をもっと大きくしても大砲の砲弾は戻って来ます。

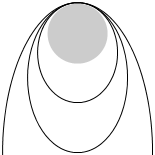ただしその軌道は楕円になります。

初速を大きくしていけばそれだけ大きな楕円になります。

そしてさらに初速を大きくしていくと、軌道は楕円でなく放物線になります。つまり無限の彼方に飛び出していってしまいます。地球の引力を振り切るのです。

このときの初速を求めてみます。力学的エネルギー保存の法則を用います。

万有引力は保存力であるから力学的エネルギー保存の法則が成り立っています。万有引力は位置のみによって決まる量＊「位置のみ」といいますか、「距離のみ」です。地球の質量、砲弾の質量が定まっていれば、地球の重心と砲弾の重心との「距離」だけで万有引力の大きさは決まります。
そもそも 重力＝万有引力 であり、重力が保存力なのだから万有引力も保存力です。
保存力としてイメージしにくいのは、重力や弾性力と違って、力の方向が刻々と変わるからだと思います、が、それでも「距離」だけで決まるので保存力です。
　閉じるなので保存力であり、今は空気抵抗が無いという前提であり大砲の砲弾には保存力のみがはたらいているので力学的エネルギー保存の法則が成り立ちます。

力学的エネルギーとは運動エネルギーと位置エネルギーの和のことであり、それが保存されるということは、運動エネルギーと位置エネルギーの和が一定、ということです。

初速度を v₀ 、地球の中心と砲弾との距離を r としますと、以下のように表せます。

　　　　\(\large{\frac{1}{2}}\)mv₀² + \(\Bigl(-G\large{\frac{Mm}{R}}\)\(\Bigr)\) = \(\large{\frac{1}{2}}\)mv² + \(\Bigl(-G\large{\frac{Mm}{r}}\)\(\Bigr)\)　　……②

左辺はスタートの瞬間の力学的エネルギーです。左辺第1項が大砲が砲弾に与えた運動エネルギーで、左辺第2項が万有引力による位置エネルギーです。右辺は任意の点における力学的エネルギーです。この力学的エネルギーが一定ということです。

砲弾は発射されたときに運動エネルギーが最大で位置エネルギーが最小です。発射されたあと、徐々に運動エネルギーが減少して位置エネルギーが増加し、最も遠い地点で運動エネルギーが最小、位置エネルギーが最大、となります。砲弾の初速をどんどん大きくしていけば楕円軌道も無限大に近い大きさになっていきます。このときの最も遠い地点、つまり運動エネルギーが最小になる地点において少しでも運動エネルギーがある、すなわち少しでも速さがあれば、それは楕円軌道を飛び出す、ということになります。これが地球の引力を振り切るという状態です。

これは②式において、右辺第2項の r が ∞ 、つまり右辺第2項 \(\Bigl(-G\large{\frac{Mm}{r}}\)\(\Bigr)\) が 0 で、右辺第1項が \(\large{\frac{1}{2}}\)mv² ≧ 0 ということです。つまり、

　　　　\(\large{\frac{1}{2}}\)mv₀² + \(\Bigl(-G\large{\frac{Mm}{R}}\)\(\Bigr)\) = \(\large{\frac{1}{2}}\)mv² ≧ 0

　∴　　\(\large{\frac{1}{2}}\)mv₀² + \(\Bigl(-G\large{\frac{Mm}{R}}\)\(\Bigr)\) ≧ 0

　∴　　\(\large{\frac{1}{2}}\)mv₀² ≧ \(G\large{\frac{Mm}{R}}\)

　∴　　v₀² ≧ \(\large{\frac{2GM}{R}}\)

　∴　　v₀ ≧ \(\sqrt{\large{\frac{2GM}{R}}}\)　　GM = gR² を代入して

　∴　　v₀ ≧ \(\sqrt{2gR}\)

となります。このときのぎりぎり振り切る速さ　v = \(\sqrt{2gR}\)　を第2宇宙速度（あるいは脱出速度）といいます。

この速度は第1宇宙速度の \(\small{\sqrt{2}}\) 倍になっています。つまり、\(\small{\sqrt{2}}\)×7.9 ≒ 1.41×7.9 ≒ 11 km/s です。

この速さ以上で大砲を撃てば、砲弾は地球の引力を振り切って遥か彼方まで飛んでいきます。上で挙げた数値の例でいいますと、運動エネルギーと位置エネルギーの和が -250J とか -280J ではなく 0J とか 10J とかプラスになった状態です。

ちなみに、人工衛星は地球の引力を振り切って脱出すると、今度は太陽の引力に捕まって太陽の周りを回り出します。すると「人工衛星」という名前でなくなり「人工惑星」という呼び名に変わります。恒星（太陽）の周りを回るのが惑星で、惑星の周りを回るのが衛星です。人工衛星と人工惑星を総称して「人工天体」と呼びます。

また、第1宇宙速度、第2宇宙速度の他に第3宇宙速度というものもあります。