人工衛星_補足

第1宇宙速度の別の導出方法

本編では円運動の運動方程式を用いて第1宇宙速度を導出しましたが、運動方程式を使わず三平方の定理を用いて近似的に導出する方法もあります。

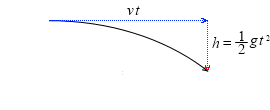物体を初速度 v で水平投射すると、水平方向に vt 進み、鉛直方向に h = \(\large{\frac{1}{2}}\)gt² だけ落下します。軌道はカーブを描きます。

もしこのカーブが地球のまるみと一致していれば物体は地表すれすれを落下し続けることになります。そして結局地球を一周します。

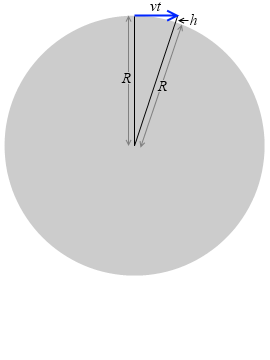t 秒後の物体が地表すれすれの位置にいたとします。つまり軌道のカーブと地球のまるみが一致していたとします。すると左図のようになります。

地球の半径を R としますと、三平方の定理より、

　　(vt)² + R² = (R + h)²

∴　(vt)² + R² = R² + 2Rh + h²

∴　(vt)² = 2Rh + h²　　h は R に比べて十分小さいので h² は無視

∴　(vt)² = 2Rh　　h = \(\large{\frac{1}{2}}\)gt² だから

∴　(vt)² = 2R⋅\(\large{\frac{1}{2}}\)gt²

∴　(vt)² = R⋅gt²

∴　v² = gR

∴　v = \(\sqrt{gR}\)

となり、本編と同じ結果が得られます。この初速度で物体を水平投射すると、落下しながら地球を一周します。もちろん空気抵抗が無いという前提です。

大砲を持ち出す理由

本編の説明において、例として「ロケット」や「ミサイル」を持ち出さず、なぜ「大砲」を持ち出したのかといいますと、それは、物体に初速を与えたら、後は慣性飛行するというイメージを持ってもらいたかったからです。第1宇宙速度、第2宇宙速度というものは初速度のことです。発射した後は万有引力以外の力が加わらないという設定の話です。「ロケット」や「ミサイル」だと、飛行中も自力で加速します。ですので宇宙速度の話で例として持ち出すのは不適切です。

静止軌道は赤道上空ですが

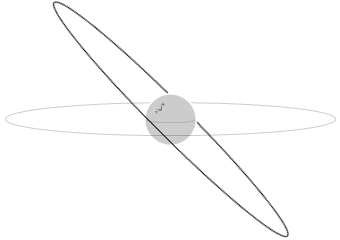静止軌道の説明において、それは赤道上空であると説明しましたが、これは地上から見たときに人工衛星が静止して見えるようにするためであり、地球と同じ角速度で回るというだけならば赤道上空でなくてもいいです。それは軌道傾斜角が斜めになってしまうような軌道ですが、高度が3万6000 km でありさえすれば地球と同じ角速度で回ります。このような軌道にある人工衛星は地上から見ると北に行ったり南に行ったりするように感じます。

スペースシャトル

アメリカのスペースシャトル事業はすでに廃止されてしまいましたが、その報道を見ているとき「スペースシャトルは90分で地球を一周する」とよく言われていました。静止衛星が24時間で一周ですからそれより相当速いわけです＊このとき、いくらスペースシャトルといえども、自力航行していたとは思えません。万有引力にまかせて慣性飛行していたはずです。
　閉じる。そして本編で人工衛星の速さは高度による、高いほど遅いと説明しました。としますと、相当速いスペースシャトルは結構低い高度を飛んでいたことになります。調べてみますと、高度200~400km程度だったようです。速さは 7.7km/s ぐらいだったようです。この数値は第1宇宙速度とあまり変わりません。スペースシャトルは結構地表すれすれを飛んでいたということです。

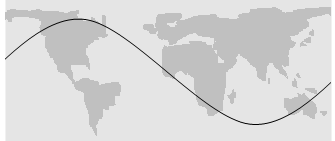またその軌道を紹介する映像で左図のように蛇行した軌道がよく映っていました。

スペースシャトルは赤道上空ではなく、ある程度の傾斜角がある軌道を回っていたと考えられます。

あと機体にコリオリ力がはたらいていたと考えられますが、90分で一周ということは結構なコリオリ力だと思いますが、どうやって姿勢を制御していたのか気になります。（機体が回転してしまっても上等だったか、細長い機体ならコリオリ力の影響を受けないのか。）

高高度の脱出速度

本編で説明した第2宇宙速度は、地表の位置から大砲を撃つ場合の話でしたが、もし、もっと高い高度から大砲を撃つ場合は、もうちょっと小さい速度で地球の引力から脱出することができます。

高さ h の高度から大砲を撃つ場合は、本編で示した力学的エネルギー保存の法則の式

　　　　\(\large{\frac{1}{2}}\)mv₀² + \(\Bigl(-G\large{\frac{Mm}{R}}\)\(\Bigr)\) = \(\large{\frac{1}{2}}\)mv² ≧ 0

の左辺第2項が　\(\Bigl(-G\large{\frac{Mm}{R}}\)\(\Bigr)\)　ではなく　\(\Bigl(-G\large{\frac{Mm}{R+h}}\)\(\Bigr)\)　となりますので、

　⇒　　\(\large{\frac{1}{2}}\)mv₀² + \(\Bigl(-G\large{\frac{Mm}{R+h}}\)\(\Bigr)\) ≧ 0

　∴　　\(\large{\frac{1}{2}}\)mv₀² ≧ \(G\large{\frac{Mm}{R+h}}\)

　∴　　v₀² ≧ \(\large{\frac{2GM}{R+h}}\)

　∴　　v₀ ≧ \(\sqrt{\large{\frac{2GM}{R+h}}}\)

となり、分母に h がある分、v₀ は小さくなります。高さがあるときは脱出に必要な速度が第2宇宙速度より小さくて済むのです。

力学的エネルギーのグラフ

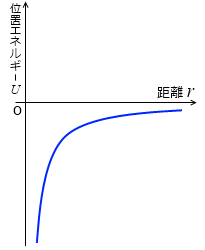『万有引力による位置エネルギー』において左図のようなグラフを示しました。この位置エネルギーに運動エネルギーを加えたものが力学的エネルギーです。

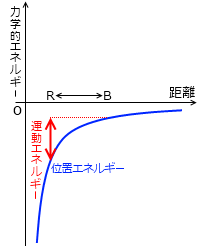運動エネルギーが足りなくて脱出できないときというのは、力学的エネルギーが 0 を超えていない状態で、グラフのR点からB点を行ったり来たりしている状態です。

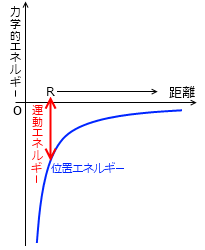運動エネルギーが十分与えられて力学的エネルギーが 0 をちょっとでも超える場合は、大砲の砲弾は地球の引力を振り切って無限の彼方に飛び立つことができます。

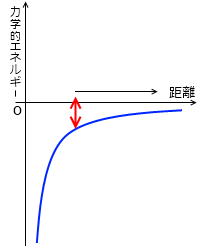高い高度から大砲を撃つときは、元々の位置ネルギーが大きいので、与える運動エネルギーが小さくても地球の引力を振り切れます。

第2宇宙速度の向き

本編での説明では第2宇宙速度の向きについて、第1宇宙速度の説明の流れから水平方向でなくてはならないかのような印象を与えてしまったと思いますが、これは本当はどっち向きでもかまいません。必要なだけの運動エネルギーを与えさえすればいいです。

地球は東向きに自転していますので、東向きに大砲を撃てば自転速度を利用する分、多少脱出に有利になります。

第3宇宙速度

本編で第1宇宙速度と第2宇宙速度について説明しましたが、第3宇宙速度というものもあります。これは、大気の無い地球から大砲を撃ったときに、その砲弾が地球の引力だけでなく太陽の引力をも振り切る速度のことです。

たぶんこれは高校物理の範囲外だと思いますので、概要だけ説明します。

第2宇宙速度を求めた式　v₀ ≧ \(\sqrt{\large{\frac{2GM}{R}}}\)　の M のところに太陽の質量を代入、R のところに地球の公転半径を代入して、太陽の引力を振り切る速度を導き出します。すると 約42km/s となります。これが第3宇宙速度であれば単純でいいのですが、第3宇宙速度の定義はもうちょっと複雑です。

この 42km/s から地球の公転速度を引きます。地球の公転運動によって助走がつけられていると考えるからです。

地球の公転速度は、人工衛星の速さを求めた式　v = \(\sqrt{\large{\frac{GM}{R+h}}}\)　の M のところに太陽の質量を、R + h のところに地球の公転半径を代入して求めます。すると 約30km/s となります。（これを\(\sqrt{2}\)倍すると 42km/s になるのですが。）

42 - 30 = 12 km/s 。これが第3宇宙速度です、といいたいところですが、まだだめです。

地球から大砲を撃って、地球の引力で減速してもなお 12km/s の速度を保つような速度でなければなりません。それが第3宇宙速度です。

第2宇宙速度を求めたときの②式

　　　　\(\large{\frac{1}{2}}\)mv₀² + \(\Bigl(-G\large{\frac{Mm}{R}}\)\(\Bigr)\) = \(\large{\frac{1}{2}}\)mv² + \(\Bigl(-G\large{\frac{Mm}{r}}\)\(\Bigr)\)

において、地球から十分離れたとき（r が十分大きくなったとき）、つまり右辺第2項　\(\Bigl(-G\large{\frac{Mm}{r}}\)\(\Bigr)\)　が 0 になったときに、右辺第1項の v が 12km/s になっていることが必要です。つまり、

　　　　\(\large{\frac{1}{2}}\)mv₀² + \(\Bigl(-G\large{\frac{Mm}{R}}\)\(\Bigr)\) = \(\large{\frac{1}{2}}\)m⋅12² + 0

が成り立つような v₀ でなければなりません。そうしますと、 v₀ ≒ 17 km/s　となります。これが第3宇宙速度です。この速度で大砲を撃てば、砲弾は太陽系外に飛び出すことができます。