重心
重心
重心とは大雑把にいうと、物体（剛体）の中心、ということになりますが、その中心という場所をどう考えるかといいますと、重さ（重力）を考慮したときにその点を支えると全体を支えることができる点ということになります。重さ的にバランスのとれる点です。
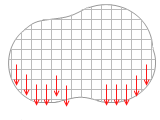剛体を小部分に分割して考えると、各部分には小さな重力がはたらいています。
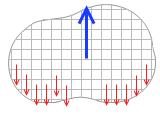重心を支えると各部分の重力を支えることができるわけです。
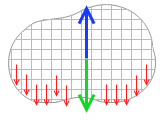その上向きの支える力と逆向きの力というのは各部分の重力を合成したもののはずです。各部分の重力の反対が上向きの支える力でその反対が逆向きの力なのだから、各部分の重力と逆向きの力というのは同じものであるという論理です。『平行で同じ向きの2力の合成』の「赤い2力に対抗してつり合う力がピンクの力で、赤い2力の合力はそのピンクの力と逆向きであるはず」という論法とまったく同じです。
つまり重心の位置というのは、各部分にはたらく重力を合成してできた合力の作用点の位置、ということになります。
そして、各部分にはたらく重力というのは、すべて鉛直下向きで同じ方向を向いています。つまり平行です。平行な力を合成するということは前項の『平行で同じ向きの2力の合成』にのっとって、2力ずつ合成していくということです。前項の説明文を読み返してもらえるとわかると思いますが、合力の大きさは各部分の重力の大きさの和となりますし（前項でいうと、F1+2 = F1 + F2）、重心における各部分の重力のモーメントの和は 0 です（前項でいうと、点Cのまわりの力のモーメントの和 F1×l1 - F2×l2 = 0 ）。
問題は、前項でいうところの2力の逆比に内分する点というものがどのような点であるかです。
重心の位置の式
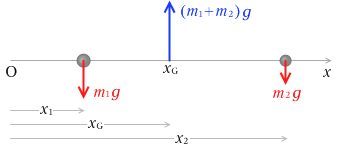まず、2つの物体の重心の位置について考えてみます。水平な x軸の x1 の位置に質量 m1 の物体、x2 の位置に質量 m2 の物体があり、2つの物体の距離は固定されているものとします。そして、xG の位置に重心があり、この位置に架空の上向きの力がはたらいていて、2つの物体の重力とつり合って静止しているとします。
前項の『平行で同じ向きの2力の合成』と同じように考えると、xG の回りの力のモーメントは 0 だから、
(m1+m2)g×0 + m1g(xG-x1) - m2g(x2-xG) = 0
∴ m1g(xG-x1) = m2g(x2-xG) ……(i)
試験等で問題を解くときは架空の上向きの力のことは考えずに、
「 xG の回りの力のモーメントを考えると m1g(xG-x1) - m2g(x2-xG) = 0 」
といきなりやってしまっていいと思います。もっといえば、
「 重心の左右でつり合っている（天秤がつり合っている）はずだから m1g(xG-x1) = m2g(x2-xG) 」
とやってしまっても大丈夫かもしれません。
(i)式の両辺を g で割りますと、
m1(xG-x1) = m2(x2-xG)
⇒ m1xG - m1x1 = m2x2 - m2xG
⇒ m1xG + m2xG = m1x1 + m2x2
⇒ (m1 + m2)xG = m1x1 + m2x2
これをさらに変形すると以下のようになります。
2物体の重心の位置の式
xG = \(\large{\frac{m_1x_1\ +\ m_2x_2}{m_1\ +\ m_2}}\)
物体が2個でなくn個の場合は、
重心の位置の式
xG = \(\large{\frac{m_1x_1\ +\ m_2x_2\ +\ \ \cdots\ +\ m_nx_n}{m_1\ +\ m_2\ +\ \ \cdots\ +\ m_n}}\)
さらに、x軸上だけでなく、平面的（2次元的）に広がっている場合は、y方向についても同様に表せます。
重心の位置の式
yG = \(\large{\frac{m_1y_1\ +\ m_2y_2\ +\ \ \cdots\ +\ m_ny_n}{m_1\ +\ m_2\ +\ \ \cdots\ +\ m_n}}\)
吊るすと分かる
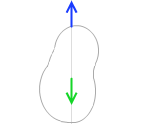剛体の1点を糸で吊るして静止したとき、重心は糸の張力の作用線上にきます。重心が作用線上にないときはバランスがとれず剛体が動いてしまいます。静止してつり合っているときというのは張力の作用線上のどこかに必ず重心があるのです。
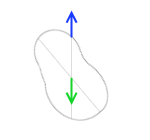ということは、糸を結ぶ位置をずらしてもう一度吊るしたとき、先ほどの作用線との交点が重心となるということです。2つのそれぞれの作用線の上に重心がある、という条件を満たす位置というのは、その2つの作用線の交点だけだからです。
このことはさらにいうと、重心の位置を特定するためには3回位置を変えて吊るす必要はないということです。2回で特定できるということです。3回やったとしても3回目も同じ位置が作用線上にきます。
一応ことわっておきますが、重心は2箇所に存在することはありません。上で、各部分の重力を合成した合力の作用点が重心であると説明しましたが、各部分の重力は前項の『平行で同じ向きの2力の合成』にのっとって必ず合成することができます。ですので次々に足し合わせていくと必ず1つの合力となります。よって、重心は必ず1つです。
物体が2つのときの重心というものはどうとらえればいいんだ、とお思いになるかもしれません。たとえば、鉄球Aと鉄球Bがあって、そのときの重心は鉄球Aと鉄球Bの間のどこかにあるわけですが、この重心はあくまでも1箇所です。これは鉄球Aと鉄球Bの2つに着目したときの話です。もし、鉄球Aだけに着目するならその重心は鉄球Aの中心付近のどこかにただ1箇所あります。鉄球Bだけに着目するならその重心は鉄球Bの中心付近のどこかにただ1箇所あります。重心というものは着目のしかたによって変わり、その着目のしかたごとに1箇所だけ存在します。
様々な形の物体の重心
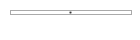一様な棒の重心はその中点にあります。一様な、というのは密度がどこも一定で均一という意味です。
一様な円板、一様な球の重心はその中心にあります。
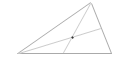三角形の板の重心は、その中線（頂点と対辺の中点を結ぶ線分）の交点（中線を頂点から 2:1 に内分した点）にあります。
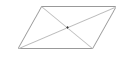平行四辺形の板の重心は、その対角線の交点（対角線の中点）にあります。
以上は物理というより数学分野の問題です。
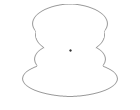対称軸のある物体の重心は、その対称軸上にあります。このことは物理の問題を解くときによく使います。
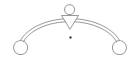また、やじろべえの重心は、物体外（空中）にあります。