剛体にはたらく力の合成

複雑

力の合成については『力の合成・分解』にて説明しましたが、それは質点にはたらく力についてのものであり、単純でした。本項で説明する剛体にはたらく力についての合成はちょっと複雑です。

• 平行でない2力
• 平行で同じ向きの2力
• 平行で逆向きの2力
• 平行で逆向きで大きさの等しい2力（偶力）

の４パターンに分けて説明します。

平行でない2力の合成

平行でない2力、については単純です。

作用線の定理を使って2つの力の作用点を重ねて、平行四辺形を作れば合力が求められます。この合力も作用線上を動かすことができます。

ですので、下記の５つのパターンはどれも同等です。剛体に作用する効果はどれも同じです。

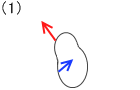
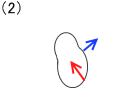
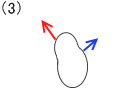
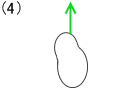
平行で同じ向きの2力の合成

力が平行な場合は作用線が交わらないので、上のような方法で合成することができません。平行な場合は合成方法が少し複雑です。

まず、同じ向きの2力の場合について考えてみます。

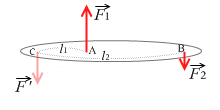
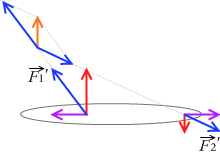
左図のように剛体に \(\vec{F_1}\)、\(\vec{F_2}\) の2力がはたらいているとし、この2力の合力を求めます。

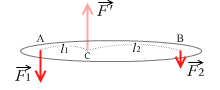まず、この2力とつり合う架空の力 \(\vec{F'}\) を考えます。つり合っているという前提でつり合いの条件を使って計算していきます。

この架空の力の大きさを求めると、つり合いの条件①より、
　　　F' - F₁ - F₂ = 0　　（どれも平行なのでベクトルではなく上向き正のスカラーとして計算しました）
　∴　F' = F₁ + F₂

また、つり合いの条件②より、点Cの回りの力のモーメントを和を考えると、
　　　F' × 0 + F₁ × l₁ - F₂ × l₂ = 0
　∴　F₁ × l₁ = F₂ × l₂
　∴　\(\large{\frac{l_1}{l_2}}\) = \(\large{\frac{F_2}{F_1}}\)
　∴　l₁：l₂ = F₂：F₁
すなわち、点Cからの（腕の長さ）の比が2つの力の大きさの逆比、要するに点Cの位置は線分ABを2つの力の逆比に内分する点になります。

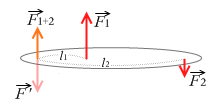
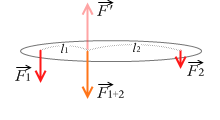そして、求める合力 \(\vec{F_{1+2}}\) は架空の力 \(\vec{F'}\) とつり合うはずですので、大きさが同じで向きが逆です。

とうわけで、左図の赤の2力は、合成するとオレンジの力となります。

赤い2力に対抗してつり合う力がピンクの力で、赤い2力の合力はそのピンクの力と逆向きであるはず、という論法です。

上と同じ答えが作図を使って求めることができます。架空の2力を加えて、平行な2力を無理やり平行でない2力にして合成する、という作戦です。

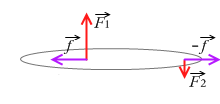
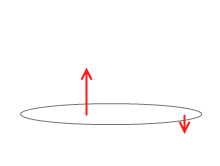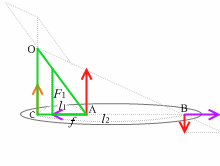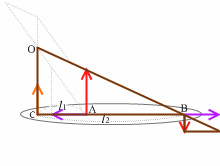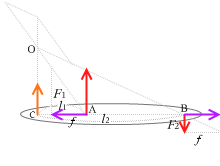
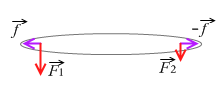剛体に架空のつり合う2力 \(\vec{f}\) 、 - \(\vec{f}\) を加えます。（好きな大きさで構いません）。これらはつり合う2力なので打ち消し合います。ですので剛体に何の影響も与えません。

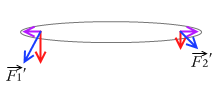これら2力を加えてできた新たな力 \(\vec{F_{1}'}\)、\(\vec{F_{2}'}\) は平行ではなくなるので合成しやすくなります。

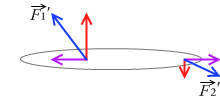
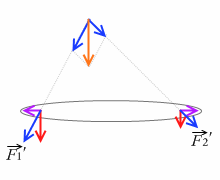新たな力 \(\vec{F_{1}'}\)、\(\vec{F_{2}'}\) を作用線上を動かして平行四辺形を作って合成すると、オレンジの合力となります。このオレンジの合力は、横方向の成分 \(\vec{f}\) 、 - \(\vec{f}\) が打ち消し合ってできたものなのでこれがまさに求める合力です。このオレンジの合力を作用線上を動かし剛体のところまで持って来れば、上での結果と一致するはずです。

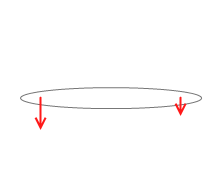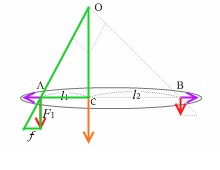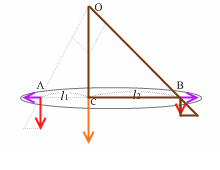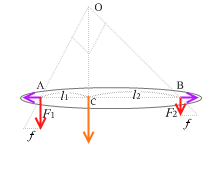左図の緑の2つの三角形は相似であるので、
　　OC : l₁ = F₁ : f
∴　F₁ × l₁ = OC × f

茶の2つの三角形は相似であるので、
　　OC : l₂ = F₂ : f
∴　F₂ × l₂ = OC × f

よって、
　　　　F₁ × l₁ = F₂ × l₂
　　∴　\(\large{\frac{l_1}{l_2}}\) = \(\large{\frac{F_2}{F_1}}\)
　　∴　l₁：l₂ = F₂：F₁
となり、点Cの位置は線分ABを2つの力の大きさの逆比に内分する点、となります。

このように作図を使った考え方でも、上でつり合いの条件を使って考えたときと結果が一致します。

平行で同じ向きの2力の合成の具体例を示します。

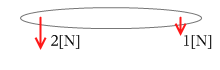左図のような2力は、合成すると、

このようになります。

平行で逆向きの2力の合成

平行で逆向きの場合の合成についても、上と同様に求めてみます。

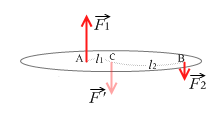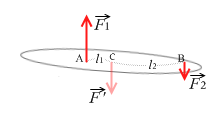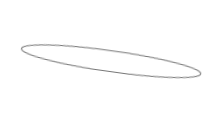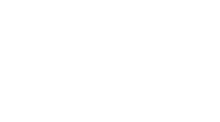
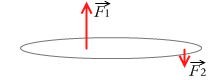左図のように剛体に \(\vec{F_1}\)、\(\vec{F_2}\) （F₁ > F₂）の2力がはたらいているとし、この2力の合力を求めます。

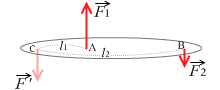まず、この2力とつり合う架空の力 \(\vec{F'}\) を考えます。つり合っているという前提でつり合いの条件を使って計算していきます。

この架空の力の大きさを求めると、つり合いの条件①より、
　　　F' - F₁ + F₂ = 0　　（どれも平行なのでベクトルではなく下向き正のスカラーとして計算しました）
　∴　F' = F₁ - F₂

また、つり合いの条件②より、点Cの回りの力のモーメントを和を考えると、
　　　F' × 0 + F₁ × l₁ - F₂ × l₂ = 0
　∴　F₁ × l₁ = F₂ × l₂
　∴　\(\large{\frac{l_1}{l_2}}\) = \(\large{\frac{F_2}{F_1}}\)
　∴　l₁：l₂ = F₂：F₁
すなわち、点Cからの（腕の長さ）の比が2つの力の大きさの逆比。

そのような点というのは左図のように線分ABを外分する点です。この点ならば「点Cからの（腕の長さ）の比が2つの力の大きさの逆比」といえます。

要するに、点Cの位置は、線分ABを2つの力の大きさの逆比に外分する点です。

そして、求める合力 \(\vec{F_{1+2}}\) は架空の力 \(\vec{F'}\) とつり合うはずですので、大きさが同じで向きが逆です。

というわけで、左図の赤の2力は、合成するとオレンジの力となります。

上の『平行で同じ向きの場合』で考えたのと同じく、赤い2力に対抗してつり合う力がピンクの力で、赤い2力の合力はそのピンクの力と逆向きであるはず、という論法です。

これと同じ答えが、上の『平行で同じ向きの場合』と同様、作図を使って求めることができます。架空の2力を加えて、平行な2力を無理やり平行でない2力にして合成する、という作戦です。

剛体に架空のつり合う2力 \(\vec{f}\) 、 - \(\vec{f}\) を加えます。これらはつり合う2力なので打ち消し合います。ですので剛体に何の影響も与えません。

これら2力を加えてできた新たな力 \(\vec{F_{1}'}\)、\(\vec{F_{2}'}\) は平行ではなくなるので合成しやすくなります。

新たな力 \(\vec{F_{1}'}\)、\(\vec{F_{2}'}\) を作用線上を動かして平行四辺形を作って合成すると、オレンジの合力となります。このオレンジの合力は、横方向の成分 \(\vec{f}\) 、 - \(\vec{f}\) が打ち消し合ってできたものなのでこれがまさに求める合力です。このオレンジの合力を作用線上を動かし剛体のところまで持って来れば、上での結果と一致するはずです。

左図の緑の2つの三角形は相似であるので、
　　OC : l₁ = F₁ : f
∴　F₁ × l₁ = OC × f

茶の2つの三角形は相似であるので、
　　OC : l₂ = F₂ : f
∴　F₂ × l₂ = OC × f

よって、
　　　　F₁ × l₁ = F₂ × l₂
　　∴　\(\large{\frac{l_1}{l_2}}\) = \(\large{\frac{F_2}{F_1}}\)
　　∴　l₁：l₂ = F₂：F₁
となり、点Cの位置は線分ABを2つの力の大きさの逆比に外分する点、となります。

このように作図を使った考え方でも、上でつり合いの条件を使って考えたときと結果が一致します。

平行で逆向きの2力の合成の具体例を示します。

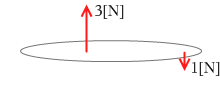左図のような2力は、合成すると、

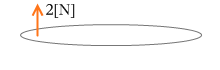このようになります。

同じ向きと逆向きのときの見比べ

剛体にはたらく平行で同じ向きの2力の合力

　大きさ　　F₁₊₂ = F₁ + F₂

　　向き　　2力と同じ向き

　　位置　　2力の逆比に内分

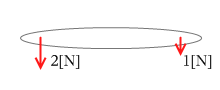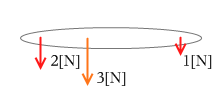
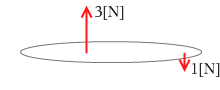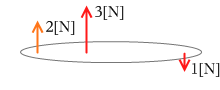
剛体にはたらく平行で逆向きの2力の合力

　大きさ　　F₁₊₂ = |F₁ - F₂|

　　向き　　大きい方の力と同じ向き

　　位置　　2力の逆比に外分

平行で逆向きで大きさの等しい2力の合成（偶力）

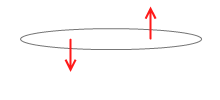実は、平行で逆向きで大きさの等しい2力の合成、はできません。2力の逆比に外分することができないのです。 l₁：l₂ = F₂：F₁ となるような点Cは無限遠の彼方になってしまいます。合成できないので合成しないまま扱い、このような2力を、1組とみなし、偶力といいます。

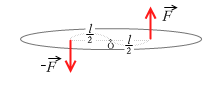2力の作用線間の距離を l とし、2力の作用線の中間にある点Oの力のモーメント M_O を求めてみます。

　　M_O = F × (\(\large{\frac{l}{2}}\)) + F × (\(\large{\frac{l}{2}}\)) = F × l　　（左回りを正としました）

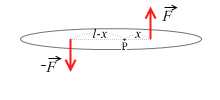これは点Oの回りではなく、任意の点の回りにおいても同じことがいえます。たとえば左図のような任意の点Pの回りの力のモーメントは、

　　M_P = F × (x) + F × (l - x) = F × l

です。

点Oの回りの力のモーメント ＝ 点Pの回りの力のモーメント ＝ F × l　です。

実はこのことは、『剛体にはたらく力のつり合い』の項の『任意の点のまわりの力のモーメントの和』においてすでに説明しています。「①式が成り立っていれば、任意の点のまわりの力のモーメントの和は変わらない」 のです。偶力はお互い同じ大きさで逆向きなのですから①式が成り立っています。こういう場合、どの点をとっても力のモーメントの和は変わらないのです。

この式 は、力が1つだけしか作用してないときの力のモーメント M = F l とまったく同じです。偶力は2つなのに1つのときと同じ？と思われてしまうかもしれませんが、よく考えると、2つであっても偶力のときは（腕の長さ）がそれぞれ半分です。（2倍）×（半分）＝ 同じ、です。

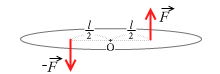このような偶力でも、

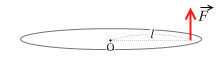このような1つの力でも、

点Oを回転させようとする力のモーメントは、どちらの場合も M = F l で、同じです。

また、偶力というのは『剛体にはたらく力のつり合い』の項の『どちらか一方を満たすとき』の「①式だけを満たすとき」に当たります。①式だけを満たして②式を満たさないというパターンは実はこの偶力のときなのです。

さらに、

偶力とは2つの力のことをいいますが、たとえ3つの力だったとしても、①式だけ満たして②式を満たさないという場合、

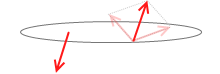そのうちの2つを1つにまとめると、残った2つは1組の偶力となります。

同じように、4つ以上の力のときでも、力をまとめていくと1組の偶力となります。