変位と速度と加速度
変位と速度と加速度
物体が運動して位置が変わったとき、その位置の変化量を変位といいます。
運動のスピードを速度といいます。
左図の物体は途中から加速しています。加速の度合いを加速度といいます。
変位と速度と加速度の関係性
速度は単位時間当たりの変位の変化量です。変位を時間で割ったものです。中学の理科で「速さは距離を時間で割ったもの」と教わったと思います。量記号は v を用います＊velocity より。閉じる。単位は [m/s]（メートル毎秒）や [km/h]（キロメートル毎時）。たとえば 3m/s といったら1秒間当たり 3m ずつ変位が増える（移動する）という意味です。
加速度は単位時間当たりの速度の変化量です。速度を時間で割ったものです。これは中学の理科では習ってないと思います。量記号は a を用います＊acceleration より。閉じる。単位は [m/s²]（メートル毎秒毎秒＊めーとるまいびょうまいびょう閉じる）や [km/h²]（キロメートル毎時毎時）。たとえば 3m/s² といったら1秒間当たり 3m/s ずつ速度が増すという意味です。
グラフで表す
次に、左図のような運動をグラフにしてみます。右向きを正とし、1目盛りを 1m とし、途中の14目盛りまでは1秒間に1目盛りずつ進み、14目盛り以降は 1m/s² ずつ加速していくものとします。
以下に、
変位と時間の関係を表す x-tグラフ、
速度と時間の関係を表す v-tグラフ、
加速度と時間の関係を表す a-tグラフ、
を順に示していきます。
x-tグラフ
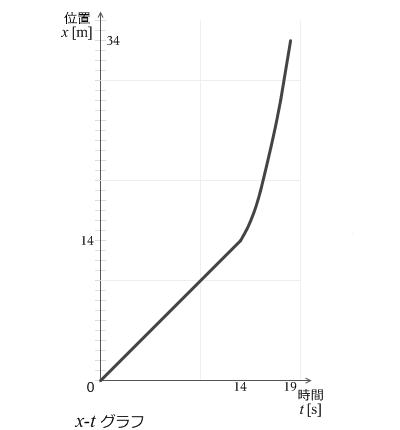左図は変位と時間の関係を表す x-tグラフです。14秒までは 1m/s の一定の速度で進んでいき、その後 1m/s² の加速度で速度が増していき、19秒で 34m の地点に達しています。
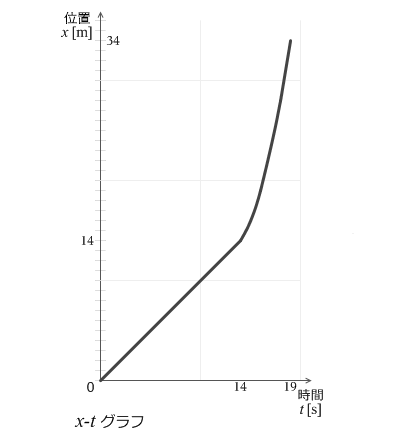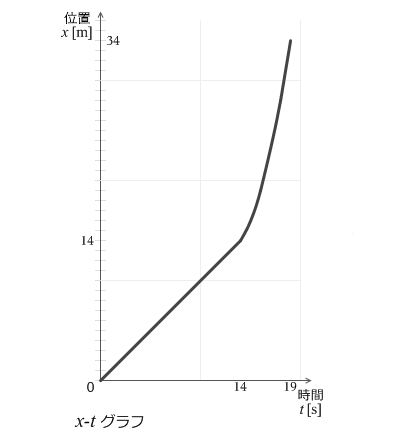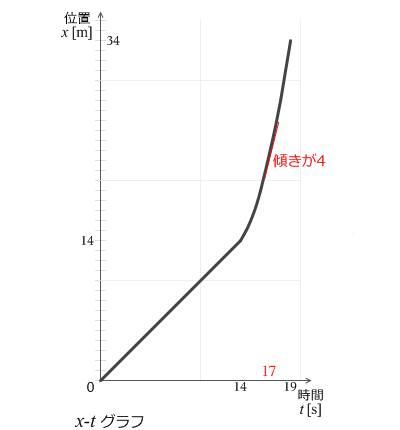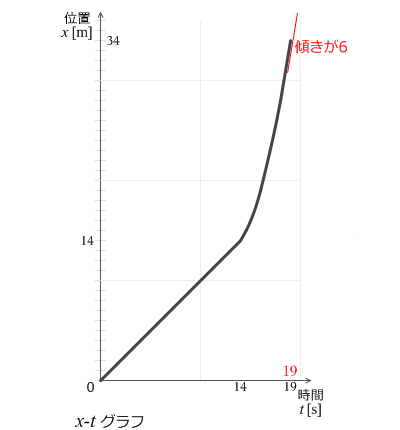グラフの傾きが速度になるというのは中学の理科でも学んだはずです。14秒までは速度が一定なので傾きも一定です。その後 1m/s² の加速度が加えられていきます。1m/s² というのは1秒に 1m/s ずつ速度が増すという意味です。時刻が
15秒のときの速度が 2m/s になり、
16秒のときの速度が 3m/s になり、
17秒のときの速度が 4m/s になり、
18秒のときの速度が 5m/s になり、
19秒のときの速度が 6m/s になります。
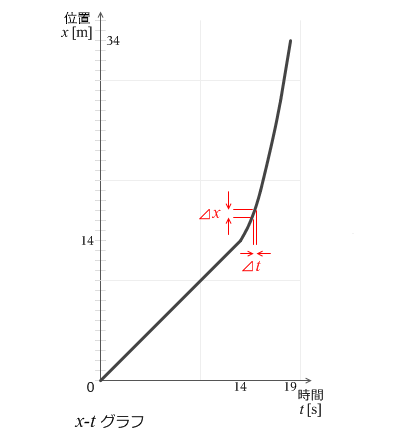14秒までのグラフは直線なので傾きは簡単に導き出せますが、それ以降のグラフは曲線なので傾きを導き出すのは難しいです。数学によれば曲線の傾きはそれぞれの点に接する接線の傾きです。そしてそれはごくごく微小な変位差 Δx をごくごく微小な時間差 Δt で割ったものです。そしてこの傾きのことを瞬間の速度といいます。
瞬間の速度 v = \(\large{\frac{\Delta x}{\Delta t}}\)
時刻が
15秒のときの瞬間の速度が 2m/s であり、
16秒のときの瞬間の速度が 3m/s であり、
17秒のときの瞬間の速度が 4m/s であり、
18秒のときの瞬間の速度が 5m/s であり、
19秒のときの瞬間の速度が 6m/s です。
v-tグラフ
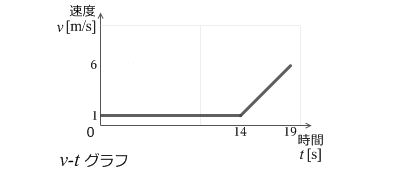左図は速度と時間の関係を表す v-tグラフです。14秒までは 1m/s の一定の速度で進んでいき、その後1秒ごとに速度が 1m/s ずつ増していき、19秒で 6m/s の速度になります。
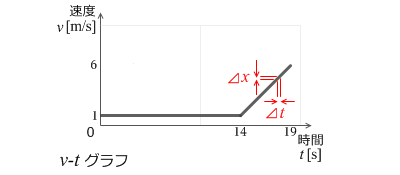このグラフの傾きは加速度を表します。14秒までは傾きが 0 です。加速度が 0 ということです。14秒から19秒までは傾きが 1 です。加速度が 1m/s² ということです。左図は曲線ではないですが曲線の場合の傾きはそれぞれの点に接する接線の傾きであり、それはごくごく微小な速度差 Δv をごくごく微小な時間差 Δt で割ったものです。そしてこの傾きのことを瞬間の加速度といいます。
瞬間の加速度 a = \(\large{\frac{\Delta v}{\Delta t}}\)
a-tグラフ
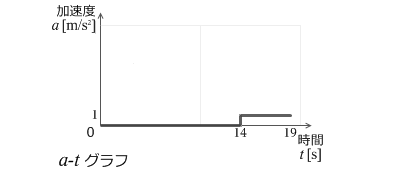a-tグラフはあまり用いられることは無いのですが、一応説明しておきますと、左図は時刻14秒までは加速度が 0 で、それ以降は加速度が 1m/s² であることを示しています。
微分・積分
変位、速度、加速度の関係は数学における微分・積分の関係になっています。数学で微分・積分を習ってない人も、いずれこの関係について学習することになるので頭に入れておいてください。
変位 →（微分）→ 速度 →（微分）→ 加速度
変位 ←（積分）← 速度 ←（積分）← 加速度
それぞれのグラフで接線の傾きを調べて瞬間の速度や瞬間の加速度を導き出すことは（微分）することに相当します。
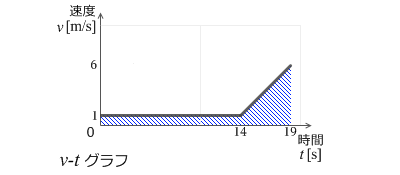また、速度を（積分）して変位を導き出すことは v-tグラフにおいて曲線と t軸に挟まれる部分の面積を求めることに相当します。
大ざっぱに面積を計算すると x = 1+1+1+1+1+1+1+1+1+1+1+1+1+1+2+3+4+5+6 = 34 となり、時刻19秒での変位は 約34m であることを示しています。
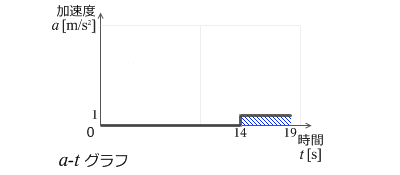また、加速度を（積分）して速度を導き出すことは a-tグラフにおいて曲線と t軸に挟まれる部分の面積を求めることに相当します。
大ざっぱに面積を計算すると v = 0+0+0+0+0+0+0+0+0+0+0+0+0+0+1+1+1+1+1 = 5 となり、時刻19秒での速度の増加は 約5m/s であることを示しています。始めの速度が 1m/s ですので時刻19秒での実際の速度は 1+5 = 6m/s です。
平均の速度
平均の速度というものを考えてみます。
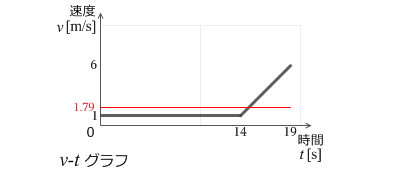v-tグラフを見ながら大ざっぱに計算すると、平均の速度 = (1+1+1+1+1+1+1+1+1+1+1+1+1+1+2+3+4+5+6)÷19 = 34÷19 ≒ 1.79 となりますが、
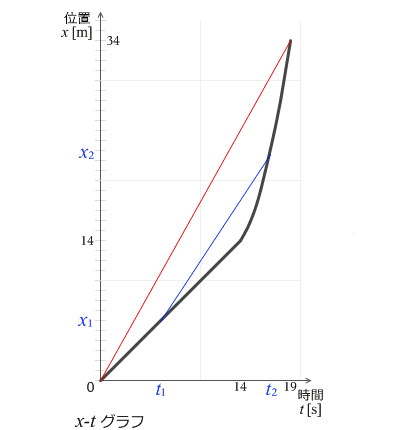この計算は左図の x-tグラフにおいて赤線の傾きを求めることと同じです。
一般的に始点と終点の変位差を経過時間で割るとその時間での平均の速度が求められます。左図の青線の傾きです。
平均の速度 \(\bar{v}\) = \(\large{\frac{x_2-x_1}{t_2-t_1}}\)
v の上のバーは平均を表す記号です。この式を見ると平均の速度は途中経路によらないことがわかります。変位差と時間差が同じであれば途中で速度が減ったりしても、その後、速度が持ち直して終点に到着しているはずだからです。
＊たとえば、A地点からB地点に時速40kmの速さで往って帰りに時速60kmでA地点に戻って来たとします。
●高校物理では、ベクトルの考え方が導入されているので、平均の速度は 0 です。A地点に戻ってきているので、変位差が 0 であるからです。
●中学理科では、スカラーでしたから、平均のスピードは時速48kmです。
中学理科では平均スピードは、（往復の道のり）を（往復の時間）で割ったものです。
往きに掛かった時間を t [h] とします。
（往復の道のり） = 40[km/h] × t[h] × 2 = 80t
（ここで往復の道のり = 40[km/h]×t [h] + 60[km/h]×t [h] とすると誤りです。帰りの時間は t ではないからです。帰りの時間は 40t÷60 [h] です。往きで確定している片道の距離 40t [km] を帰りの時速 60[km/h] で割ったものです。帰りの方が時速が速いので短い時間で済みます。帰りの道のりは 60[km/h]×(40t÷60)[h] = 40×t [km] なのです。ですので往復の道のりを 40[km/h]×t [h]×2 としたのです。中学理科の有名なひっかけ問題です。）
（往復の時間） = t [h] + (40t÷60) [h] = (100/60)t [h]
よって車の平均スピードは、
（往復の道のり）÷（往復の時間） = 80t[km] ÷ (100/60)t[h] = 4800/100[km/h] = 48[km/h]
です。往きが時速40kmで帰りが時速60kmだから足して2で割って時速50kmだ、と考えてしまうと、ひっかけポイントにハマったことになってしまいます。往きの方が車を運転している時間が長いので平均の時速は往きの値に近くなるのです。
閉じる
平均の加速度
平均の速度と同じように平均の加速度というものを考えてみます。
a-tグラフを見ながら大ざっぱに計算すると、平均の加速度 = (0+0+0+0+0+0+0+0+0+0+0+0+0+0+1+1+1+1+1)÷19 = 5÷19 ≒ 0.263となりますが、
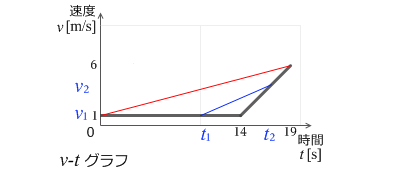この計算は左図の v-tグラフにおいて赤線の傾きを求めることと同じです。
一般的に始点と終点の速度差を経過時間で割るとその時間での平均の加速度が求められます。左図の青線の傾きです。
平均の加速度 \(\bar{a}\) = \(\large{\frac{v_2-v_1}{t_2-t_1}}\)
この式を見ると平均の加速度は途中経路によらないことがわかります。速度差と時間差が同じであれば途中で加速度が減ったりしても、その後、加速度が持ち直して終点に到着しているはずだからです。
加速度の正負
加速度というものは、自動車の運転をするようになると体感できるようになりますが、高校生にはイマイチわかりにくいことかもしれません。特に、加速度が負、というものがどういうものであるかとか、東向きを正とするときに、西向きに走っていてブレーキを踏んだときの加速度の正負、などというものはチンプンカンプンかもしれません。
いま、直線において右向きを正とします。
物体が右に移動したら変位は正です。左に移動すれば変位は負です。
右に向かって進んでいれば速度は正です。左に向かって進んでいれば速度は負です。
右に向かっていたものが更に勢いを増して右に進めば加速度は正です。
左に向かっていたものがスピードを落とし逆方向に向かい始めれば加速度は正です。
右に向かっていたものがスピードを落とし逆方向に向かい始めれば加速度は負です。
左に向かっていたものが更に勢いを増して左に進めば加速度は負です。
正の方向に持っていこうとする念力のようなものが正の加速度で、負の方向に持っていこうとする念力のようなものが負の加速度です。上図のアニメーションでは炎のイラストが目安になると思います。『等加速度直線運動』の『加速度が負の場合』もご参照ください。