保存力_補足

スタート地点に戻ると仕事は 0

保存力の中においては、A点からB点に移動させるための仕事の量は、A点の位置エネルギーとB点の位置エネルギーの差になっている、と本編で述べました。としますと、A点からB点に移動させるための仕事を W としたとき、B点からA点に移動させるための仕事は - W となります。すると、A点からB点に移動させ、さらにB点からA点に戻させるための仕事は W + ( - W ) となります。つまり 0 です。つまり、保存力の中では、スタート地点に戻ってくるとどのような経路をたどってもトータルの仕事は 0 になるのです。

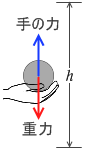球を上げ下げする例でいうと、球を持ち上げるための仕事が mgh で、球を下げるための仕事が - mgh で、トータルで仕事が 0 になる、そしてそれは経路によらない、ということです。

場

場という概念を高校物理の段階で持ち出していいのかわかりませんが、以下にそれぞれの保存力についての場のイメージを示します。

重力場。

重力場に置かれた物体の質量が大きくなると、左図の矢印も大きくなります。

（この話は地表付近での話であって、重力のおおもとの万有引力を表すイメージ図は下の静電気力の場のような図になります。）

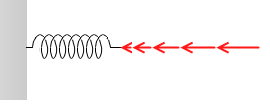弾性力の場。

基準点から離れるほど矢印は大きくなり、また、ばね定数が大きくなるほど矢印は大きくなります。

静電気力の場。

電荷に近いほど矢印は大きくなり、また、電荷が大きくなるほど矢印は大きくなります。

川の流れの場（どの地点においても流れの速さが一定の場合）。

川の流れが速かったり、船が大きかったりすると、左図の矢印も大きくなります。厳密には船の形が円形でないと保存力とはいえません。船の向きによって抵抗力の大きさが変わってきてしまうので。

また、この川の流れというものは摩擦力や空気抵抗とは根本的に違います。摩擦力や空気抵抗は、物体が動くことによって初めて発生するもので、かつ、動こうとする方向と逆向きにはたらきます。川の流れはそうではありません。（速さ一定の）川の流れは保存力でありますが、摩擦力や空気抵抗は非保存力です。

＊ ウインドカーやヨットは風に向かって進むことができますので、これまでの話と矛盾するように感じるかもしれますが、そもそも原理が違います。もしウインドカーやヨットが空中に浮いているならこれまでの話の通りですが、そうではありません。


ウインドカーはタイヤが付いていて、それが地面に引っかかります。ウインドカーは風車が存在する領域とタイヤが存在する領域で上下2層になっていると考えるべきです。上の層の風車で風を受けてそれをギアを使って大きな力に変えて下の層のタイヤを回して、元の風に対抗して進みます。



ヨットは上の層の帆（セール）で風を受けて横向きの力を得て

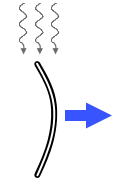
下の層のキール（船底のセンターボード）で水を切って元の風に対抗して進みます。
キールが水を切る力の掛かり方は、斜面に置かれた物体に横向きの力を加えて斜め上に持ち上げるのと似ています。

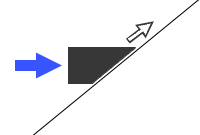
このような力の掛かり方なのでさすがに風に向かって正面に進むことはできず、ジグザグに進路をとってトータルで風上に進みます。
　閉じる