空気抵抗を受ける運動
摩擦力に似ているがちょっと違う
物体の運動を考える際には、空気抵抗については無視する場合が多いのですが、無視しない場合について、本項で説明します。
といっても、空気抵抗の大きさは、物体の形や大きさや速さによって複雑に変化し、なかなか一般化できません。本当の値は大学物理の流体力学によって導出されるのですが、高校物理では極端に単純化して考えます。空気抵抗を R[N] としますと、R = k v であるとみなします。k は比例定数です。v は物体の速さです。つまり空気抵抗は速さに比例するのです。（速さの2乗に比例 R = k v2 とする場合もあります）。
空気抵抗の向きについは、これは摩擦力とそっくりで、とにかく、運動と逆向きです。下に向かうなら上向きで、右に向かうなら左向きです。
摩擦力の大きさは、接地面との引っ掛かり具合（摩擦係数）と重さ（垂直抗力）に比例しましたが、空気抵抗の場合は、速さに比例する＊「速さに比例」といいきってしまうのはかなり乱暴ではあるのですが。
閉じるのです。速ければ速いほど空気抵抗は大きくなります。
終端速度
たとえば、地上500mの高さから重力の作用だけで落下してくる物体の、地面に到達するときの速さは、
『自由落下運動を表す式』v2 = 2 g y に代入して求めますと、
v2 = 2 × 9.8 × 500 = 9800
∴ v ≒ 99[m/s] ≒ 360 [km/h]
約時速360キロです。
しかし、地球には大気あり、空気抵抗があります。たとえば、雨滴の速さは実際には時速30キロ程度だそうです。地表付近では等速だそうです。
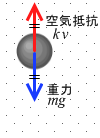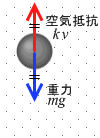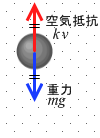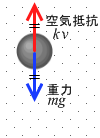
一般に、質量 m の球が空気中を落下する場合、球には鉛直下向きの重力 mg と、鉛直上向きの空気抵抗 R（=k v）がはたらき、その合力 mg - k v の力で運動します。
加速度を a（鉛直下向きが正）として運動方程式を立てますと、
ma = mg - k v
この式を解釈しますと、まず、右辺第1項の mg というのは不変です。しかし、第2項 k v は速さが増すと増えていきます。それにつれて左辺 ma は減っていきます。加速の具合が減っていくのです。だんだん k v が増えていくと、やがて mg と等しくなり、mg - k v = 0 となります。そうすると左辺 ma も 0 になるから、加速が止まります。速さが一定になるということです。速さ v が一定になればもう k v は増えなくなりますから、右辺は 0 のまま変わりません。これは（空気抵抗）k v は（重力）mg より大きくなることはないということを意味します。＊mg より大きくなることがあるとすれば、それはたとえば、上昇気流に持ち上げられるとか、静電気力が加わるとか、などといった場合です。
閉じる
このときの速度を終端速度といいます。この終端速度に達すると、球はこの速度で等速直線運動を続けます。
終端速度を求めますと、
mg - k v = 0
∴ v = \(\large{\frac{mg}{k}}\)
解釈
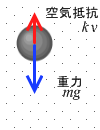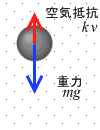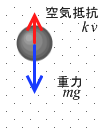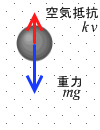
運動方程式 ma = mg - k v を、あらためてイラストを使いながら解釈してみます。
始め、初速度が 0 のうちは運動方程式の右辺第2項の k v が 0 なので、ma = mg - 0 、よって、ma = mg 、つまり加速度 a = g 。
だんだん落下速度が増していくと、右辺第2項 k v（空気抵抗）が増していき、左辺 ma が小さくなる。すなわち加速度 a が小さくなる。
さらに落下速度が増していくと右辺第2項 k v（空気抵抗）が右辺第1項 mg（重力）と等しくなり、mg - k v = 0 となり、左辺の ma も 0 となり、これはつまり加速度 a が 0 、すなわち速度が一定になるということです。
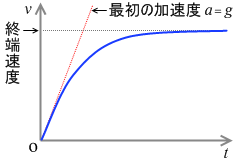縦軸を落下速度 v 、横軸を時間 t とするとグラフの曲線は左図のようになります。この曲線（青線）の傾きは加速度 a を表します。