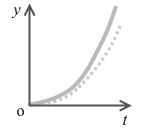
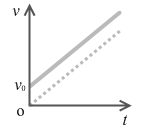
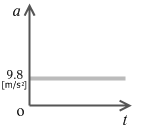鉛直上方投射の式とグラフ
鉛直下方投射とは逆に、鉛直上向きに初速を与えた運動を鉛直上方投射といいます。真上に投げ上げる運動です。始め、上方に向かい、スピードが落ちていき、やがて静止し、向きを変えて下向きに落ちていき、スピードが増していく運動です。
等加速度直線運動を表す式、
v = v0 + a t
x = v0 t + \(\large{\frac{1}{2}}\)at2
v2 - v02 = 2ax
において、v0 をそのまま、a ⇒ - g とし、x軸をy軸に変えて、鉛直上向きを正としたものが鉛直上方投射を表す式になります。(もし鉛直下向きを正としたいならば、g に - を付けないで v0 に - を付けます。)
この式は上の鉛直下方投射の式の g に - を付けたものになっています。逆にいいますと、鉛直下方投射の式は鉛直上方投射の式に統合することができます。鉛直上向きを正とし、v0 が負の値(初速が下向き)もとることとすれば、上式は鉛直下方投射も表していることになります。
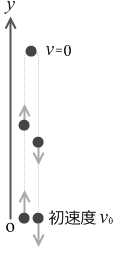
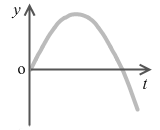
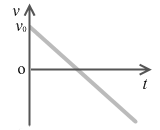
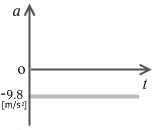
鉛直上方投射のグラフは『等加速度直線運動』の『加速度が負の場合』のグラフと同じです。
分析
上式を分析してみます。
最高点に達したときの時間を t1 とすると、このときの速度 v は 0 だから*上昇していきながら徐々にスピードが遅くなり、スピードが 0 になったときに、もうそれ以上、上にいけなくなるのだから、そのときが最高点。
閉じる、速度の式は、
v = 0 = v0 - g t1
∴ t1 = \(\large{\frac{v_0}{g}}\)
初速度 v0 が大きいほど最高点に達するまでの時間が掛かるということです。あたりまえですが。
次に、最高点を y1 とし、t1=\(\large{\frac{v_0}{g}}\) を変位の式に代入してみますと、
y = v0 t - \(\large{\frac{1}{2}}\) g t2
⇒ y1 = v0 \(\bigl(\large{\frac{v_0}{g}}\bigr)\) - \(\large{\frac{1}{2}}\) g\(\bigl(\large{\frac{v_0}{g}}\bigr)^2\)
= \(\large{\frac{{v_0}^2}{g}}\) - \(\large{\frac{{v_0}^2}{2g}}\)
= \(\large{\frac{{v_0}^2}{2g}}\)
これは、t を含まない式 v2 - v02 = - 2 g y に v=0 を代入しても求まります。
倍のスピードで投げ上げると4倍の高さまで上がります。
さらに、上がって下がって再びスタート地点に戻ってくるまでの時間(t2 とします)を求めてみます。変位の式において y=0 とおきますと、
y = v0 t - \(\large{\frac{1}{2}}\)g t2
⇒ y = 0 = v0 t - \(\large{\frac{1}{2}}\)g t2 = t ( v0 - \(\large{\frac{1}{2}}\)g t )
∴ t = 0 , \(\large{\frac{2v_0}{g}}\)
t = 0 というのはスタートしたときの時間ですから、求める時間は t2 = \(\large{\frac{2v_0}{g}}\) 。
この時間は t1 = \(\large{\frac{v_0}{g}}\) と比べると倍でありますから、つまりこれは、最高点に達するまでの時間と、最高点からスタートの位置に戻るまでの時間は等しい、ということを意味します。
また、 t2 = \(\large{\frac{2v_0}{g}}\) を速度の式に代入しますと、
v = v0 - g t
⇒ v = v0 - g \(\bigl(\large{\frac{2v_0}{g}}\bigr)\)
= v0 - 2 v0
= - v0
これはつまり、再びスタート地点に戻ってきたときの速度は、大きさが初速度と同じで向きが逆、とうことです。
『斜方投射2』もご参照ください。