運動量
物体の運動は、物体の速度が大きいほど、また、物体の質量が大きいほど、激しいといえます。よって、物体の運動の激しさを表すとき、速度と質量を掛け合わせた量を用いるのが妥当です。この量を運動量といいます。
物をぶつけて何かを壊そうとするとき、速度が大きいほど、質量が大きいほど、つまり運動量が大きいほど壊しやすいです。
運動している物体を静止させようとするとき、速度が大きいほど、質量が大きいほど、つまり運動量が大きいほど静止させにくいです。
物体の運動量を \(\vec{p}\) *なぜ量記号に p を用いるのかはっきりした起源は不明ですがラテン語の impetus あるいは petere から来ているという説があります。pet- には求める、向かうという意味があるようです。
閉じる 、質量を m [kg] 、速度を \(\vec{v}\) [m/s] 、速度の向きが運動量の向きであると定義すると以下のように表せます。
運動量
\(\vec{p}\) = m\(\vec{v}\)
運動量の単位は [kg⋅m/s] です。
この運動量という量は運動エネルギー \(\large{\frac{1}{2}}\)mv2 に似ています。違いは、速度に比例か速度の2乗に比例かということと、向きが定義されているかどうか(ベクトルかスカラーか)ということです。(『同質量、同速度で向かい合い、e = 0』参照。)
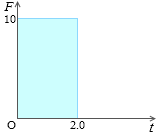 縦軸に力、横軸に時間をとったグラフにおいて、10N、2.0s のときの力積の量を表しますと、左図の青の部分の面積となります。
縦軸に力、横軸に時間をとったグラフにおいて、10N、2.0s のときの力積の量を表しますと、左図の青の部分の面積となります。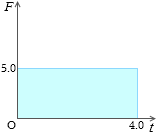 5.0N、4.0s の場合の力積を表すと左図のようになります。その面積は上図と同じです。
5.0N、4.0s の場合の力積を表すと左図のようになります。その面積は上図と同じです。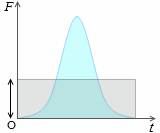 このとき力が一定でなくても、もし F-t グラフが描けるようであれば、その力積を表す面積(力の積分値)と同じ面積の長方形の縦辺の長さとして、撃力の平均の値が導き出せます。
このとき力が一定でなくても、もし F-t グラフが描けるようであれば、その力積を表す面積(力の積分値)と同じ面積の長方形の縦辺の長さとして、撃力の平均の値が導き出せます。 単純な場合(右向き正、以下同様)
単純な場合(右向き正、以下同様) 速度が減少する場合
速度が減少する場合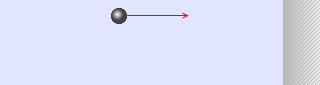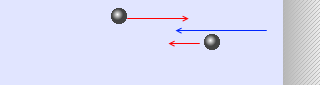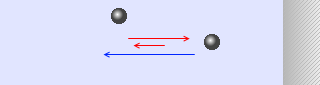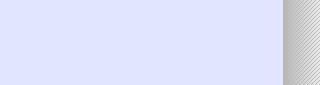 向きが 180° 変わる場合
向きが 180° 変わる場合 壁に斜めに衝突する場合
壁に斜めに衝突する場合