凸レンズのつくる像
3つの量の関係を求める
凸レンズにおいて、
物体とレンズとの距離:\(a\)
レンズと像との距離:\(b\)
焦点距離:\(f\)
の関係を考えてみます。考える光線の本数は3本ではなく2本です。2本でも各量の関係を導き出すことができます。
物体を焦点より遠くに置いたとき
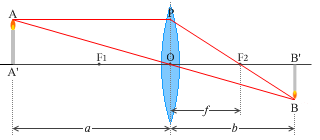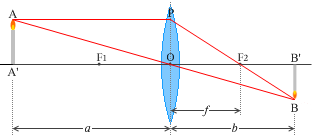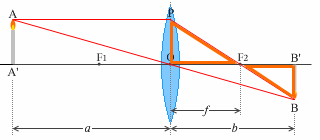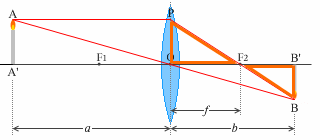 左図にように、物体から凸レンズまでの距離を \(a\) 、凸レンズから像までの距離を \(b\) 、凸レンズの焦点距離を \(f\) とします。
左図にように、物体から凸レンズまでの距離を \(a\) 、凸レンズから像までの距離を \(b\) 、凸レンズの焦点距離を \(f\) とします。
左図の赤線は、レンズによる像(凸レンズ) の(1)、(2)にのっとった線です。(3)にのっとった線は必要ないので描いてません。
△AA'O と △BB'O は相似だから、
\(\color{#b63}{{\large\rm{\frac{BB'}{AA'}}}} = {\large\rm{\frac{B'O}{A'O}}} = {\large\frac{b}{a}}\) ……①
また、AA'=PO であり、△POF2 と △BB'F2 が相似であるから、
\(\color{#b63}{{\large\rm{\frac{BB'}{AA'}}}} = {\large\rm{\frac{BB'}{PO}}} = {\large\rm{\frac{B'F_2}{OF_2}}} = {\large\frac{b\ -f}{f}}\)
よって、
\({\large\frac{b}{a}} = {\large\frac{b\ -f}{f}}\)
\(= {\large\frac{b}{f}} - 1\) 両辺を \(b\) で割って
∴ \({\large\frac{1}{a}} = {\large\frac{1}{f}} - {\large\frac{1}{b}}\)
∴ \({\large\frac{1}{a}} + {\large\frac{1}{b}} = {\large\frac{1}{f}}\) ……②
②式を レンズの公式 または 写像公式 といいます。
①を レンズの倍率 または 像の倍率 といい、\(m\) とおきます magnification(倍率)より 。
\(m = \color{#b63}{{\large\rm{\frac{BB'}{AA'}}}} = {\large\rm{\frac{B'O}{A'O}}} = {\large\frac{b}{a}}\)
これらの式を吟味してみます。
\(a > b\) すなわち \(m < 1\) のとき
②式より \(b\) を求めると、
\({\large\frac{1}{a}} + {\large\frac{1}{b}} = {\large\frac{1}{f}}\)
∴ \({\large\frac{1}{b}} = {\large\frac{1}{f}} - {\large\frac{1}{a}}\)
\(= {\large\frac{a-f}{fa}}\)
∴ \(b = {\large\frac{fa}{a-f}}\) ……③
\(a > b\) 式に代入すると、
\(a > {\large\frac{fa}{a-f}}\)
∴ \(1 > {\large\frac{f}{a-f}}\)
∴ \(a - f > f\)
∴ \(a > 2f\)
このことを図示しますと下図のようになります。
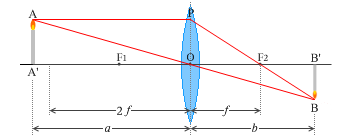 倍率を 1.0 より小さくしたい場合は、焦点距離の2倍の距離より遠くに物体を置かなければなりません。
倍率を 1.0 より小さくしたい場合は、焦点距離の2倍の距離より遠くに物体を置かなければなりません。
左図では \({\large\frac{b}{a}} = {\large\frac{3}{4}}\) ぐらいですが、像の大きさも \({\large\frac{3}{4}}\) ぐらいになってます。
\(a = b\) すなわち \(m = 1\) のとき
③式 \(b = {\large\frac{fa}{a-f}}\) を
\(a = b\) 式に代入すると、
\(a = {\large\frac{fa}{a-f}}\)
∴ \(1 = {\large\frac{f}{a-f}}\)
∴ \(a - f = f\)
∴ \(a = 2f\)
このことを図示しますと下図のようになります。
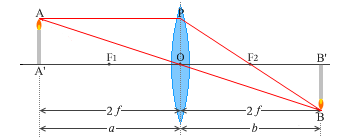 倍率を等倍にしたい場合は、焦点距離の2倍の位置に物体を置かなければなりません。
倍率を等倍にしたい場合は、焦点距離の2倍の位置に物体を置かなければなりません。
\(a = b\) で \(a = 2f\) なので \(a = 2f = b\) です。
\(a < b\) すなわち \(m > 1\) のとき
③式 \(b = {\large\frac{fa}{a-f}}\) を
\(a < b\) 式に代入すると、
\(a < {\large\frac{fa}{a-f}}\)
∴ \(1 < {\large\frac{f}{a-f}}\)
∴ \(a - f < f\)
∴ \(a < 2f\)
このことを図示しますと下図のようになります。
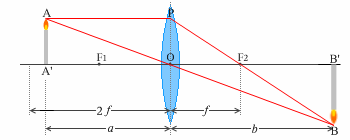 倍率を 1.0 より大きくしたい場合は、焦点距離の2倍の距離より近くに物体を置かなければなりません。
倍率を 1.0 より大きくしたい場合は、焦点距離の2倍の距離より近くに物体を置かなければなりません。
左図では \({\large\frac{b}{a}} = {\large\frac{4}{3}}\) ぐらいですが、像の大きさも \({\large\frac{4}{3}}\) ぐらいになってます。
3パターンまとめて図示してみます。
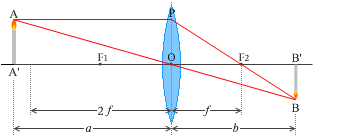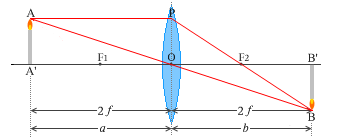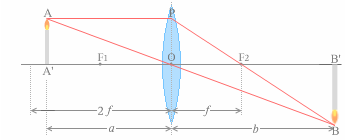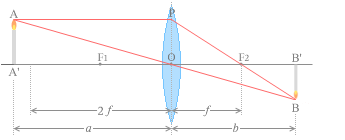 物体(AA')を置く位置によって像(BB')の大きさが変わります。
物体(AA')を置く位置によって像(BB')の大きさが変わります。
物体を焦点より近くに置いたとき
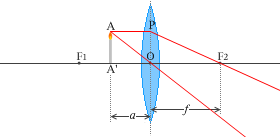 物体を凸レンズの焦点より近くに置いた場合は、光線は発散してしまって、レンズの向こう側に像を結ぶことはなくなります。スクリーンを置いても、ろうそくかどうかわからない赤っぽい色がボヤーっと映っているだけです。
物体を凸レンズの焦点より近くに置いた場合は、光線は発散してしまって、レンズの向こう側に像を結ぶことはなくなります。スクリーンを置いても、ろうそくかどうかわからない赤っぽい色がボヤーっと映っているだけです。
しかし、このようなことになってしまったときは別のことが起こります。
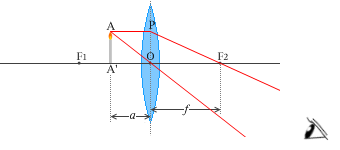 レンズの向こう側(物体を置かない方の側。F2側)からレンズの方を見ると、拡大された物体が見えるのです
(正確な言い方をすると)人間にとって拡大されたように感じます。
レンズの向こう側(物体を置かない方の側。F2側)からレンズの方を見ると、拡大された物体が見えるのです
(正確な言い方をすると)人間にとって拡大されたように感じます。
目の錯覚であるともいえます。
。
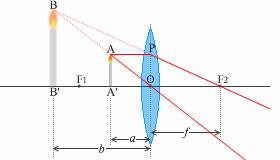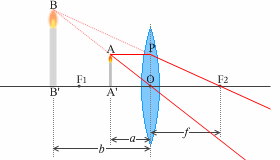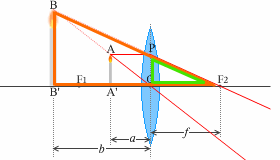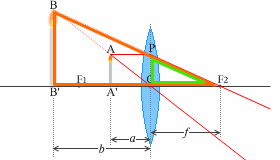 レンズによる像(凸レンズ) の(1)にのっとって考えてみますと、点Aから点Pに向かう光線は点F2を通ります。(2)にのっとって考えますと、点Aから点Oに向かう光線はそのまま真っ直ぐ進みます。この2つの光線はあたかも点Bから出ているように見えます。つまり、レンズの向こう側からレンズを通してろうそくを見ると、拡大したBB'が存在するかのように見えるのです。
人間は複数の視点から見た像を脳内で瞬時に計算して距離感をつかみます。
レンズによる像(凸レンズ) の(1)にのっとって考えてみますと、点Aから点Pに向かう光線は点F2を通ります。(2)にのっとって考えますと、点Aから点Oに向かう光線はそのまま真っ直ぐ進みます。この2つの光線はあたかも点Bから出ているように見えます。つまり、レンズの向こう側からレンズを通してろうそくを見ると、拡大したBB'が存在するかのように見えるのです。
人間は複数の視点から見た像を脳内で瞬時に計算して距離感をつかみます。

左右2つの目を使います。
数メートルほどの距離ならば片目だけでも距離感をつかめます。瞳(網膜)に大きさがあるからです。
しかし夜空の星の距離感はつかめません。数万光年の距離に対して人間の左右の目の距離、あるいは瞳の大きさが小さすぎるからです。もし瞳の大きさが地球の大きさくらいあれば星の距離感もつかめるかもしれません。
この像は人間が脳内で感じる像であり、スクリーンを置いても映し出されません。このような像を虚像といいます。そしてこれは倒立像ではなく、正立像です。
\(a\) 、\(b\) 、\(f\) の関係を求めます。
△AA'O と △BB'O は相似だから、
\(\color{#b63}{{\large\rm{\frac{BB'}{AA'}}}} = {\large\rm{\frac{B'O}{A'O}}} = {\large\frac{b}{a}}\)
また、AA'=PO であり、△POF2 と △BB'F2 が相似であるから、
\(\color{#b63}{{\large\rm{\frac{BB'}{AA'}}}} = {\large\rm{\frac{BB'}{PO}}} = {\large\rm{\frac{B'F_2}{OF_2}}} = {\large\frac{b\ +f}{f}}\)
よって、
\({\large\frac{b}{a}} = {\large\frac{b\ +f}{f}}\)
\(= {\large\frac{b}{f}} + 1\) 両辺を \(b\) で割って
∴ \({\large\frac{1}{a}} = {\large\frac{1}{f}} + {\large\frac{1}{b}}\)
∴ \({\large\frac{1}{a}} - {\large\frac{1}{b}} = {\large\frac{1}{f}}\) ……④
この式において、\(f > 0\) であるから右辺は正でありすなわち左辺も正であるので、
\({\large\frac{1}{a}} - {\large\frac{1}{b}} > 0\)
∴ \({\large\frac{1}{a}} > {\large\frac{1}{b}}\) \(b > 0\) であるから
∴ \({\large\frac{b}{a}} > 1\)
\(m = {\large\frac{b}{a}}\) であるので、すなわち \(m > 1\) 、つまりこれは、虚像は常に拡大される、ということです。
凸レンズのまとめ
②式と④式は、+ の部分と - の部分が違うだけです。物体を焦点より近くに置く場合(すなわち凸レンズで虚像ができる場合)のときの \(b\) の値を負とすれば、2つの式は1つにできます。
\({\large\frac{1}{a}} + {\large\frac{1}{b}} = {\large\frac{1}{f}}\)
\(m = {\large\frac{|b|}{a}}\)
レンズ後方に実像ができるときは \(b > 0\)
レンズ手前に虚像ができるときは \(b < 0\) ……⑤
次項で、この式が凹レンズにも拡張できることを示します。
物体を置く位置によって像がどのように変わるか、以下にまとめて描いてみます。

全コマ書き出してみます。大きい●が焦点です。ろうそくを置く位置は \({\large\frac{1}{4}}f\) ずつレンズに近づいていってます。
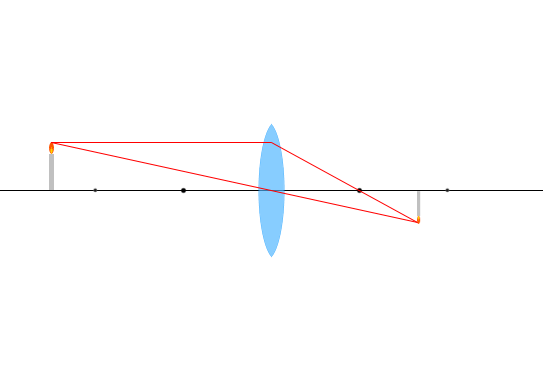 \(a > 2f\) 、 \(m < 1\)
\(a > 2f\) 、 \(m < 1\)
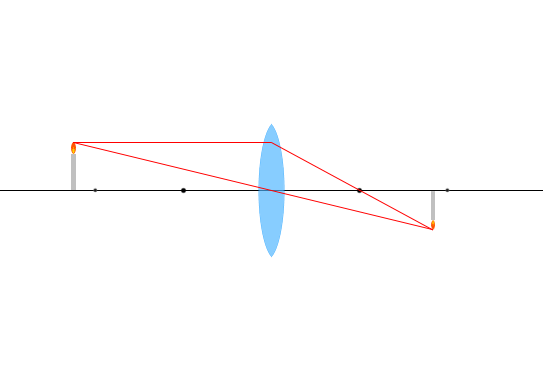 \(a > 2f\) 、 \(m < 1\)
\(a > 2f\) 、 \(m < 1\)
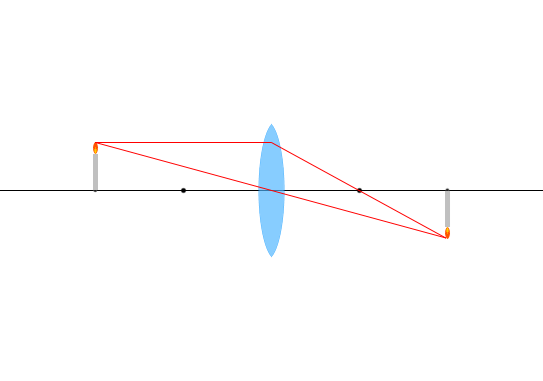 \(a = 2f\) 、 \(m = 1\)
\(a = 2f\) 、 \(m = 1\)
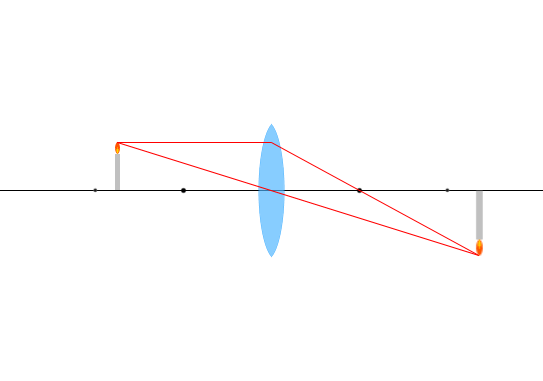 \(f < a < 2f\) 、 \(m > 1\)
\(f < a < 2f\) 、 \(m > 1\)
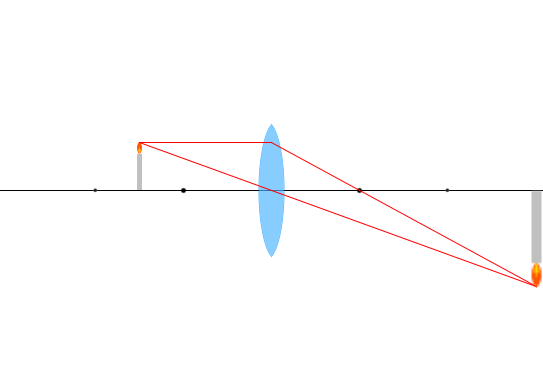 \(f < a < 2f\) 、 \(m > 1\)
\(f < a < 2f\) 、 \(m > 1\)
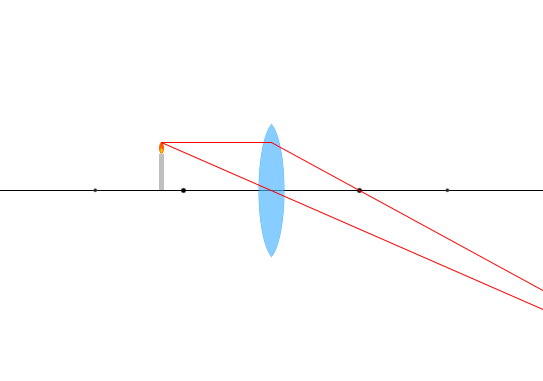 \(f < a < 2f\) 、 \(m > 1\) 像が無いわけではありません。枠内に描ききれてないだけです。
\(f < a < 2f\) 、 \(m > 1\) 像が無いわけではありません。枠内に描ききれてないだけです。
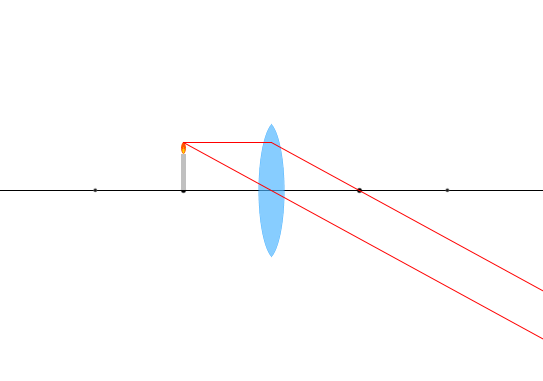 \(a = f\) 、 \(m = ∞\) 赤線が平行です。
\(a = f\) 、 \(m = ∞\) 赤線が平行です。
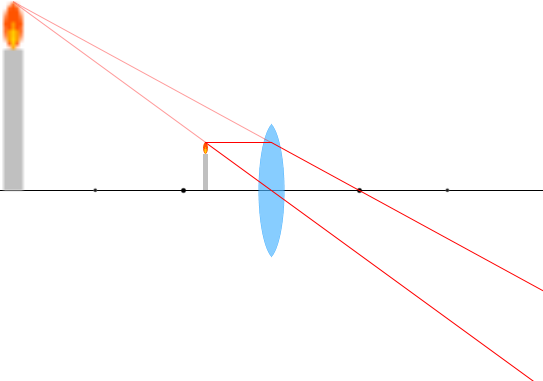 \(a < f\) 、\(b < 0\)
\(a < f\) 、\(b < 0\)
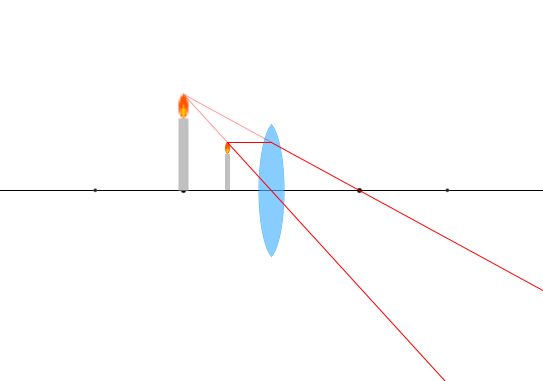 \(a = {\large\frac{1}{2}}f\) 、\(|b| = f\)
\(a = {\large\frac{1}{2}}f\) 、\(|b| = f\)
\({\large\frac{1}{a}} + {\large\frac{1}{b}} = {\large\frac{1}{f}}\) に \(a = {\large\frac{1}{2}}f\) を代入すると
\(b = - f\) になります。