気柱の振動
気柱の固有振動
シリンダーの口の部分に息を吹きかけると音が鳴ることがあります。これは内部の柱状の空気、気柱が固有振動を起こして音を出しているためです。リコーダーやクラリネットなどの管楽器も同じ原理で音を出しています。 気柱共鳴と混同しやすいものにヘルムホルツ共鳴 Wikipediaというものもあります
前項では弦の固有振動について考えましたが、本項では気柱の固有振動について考えます。
気柱を考えるときの管の種類には、
一方が閉じてもう片方が開いた閉管と、
両端が開いた開管とがあります。
両方閉じた管のことはあまり考えません。これは前項の弦の固有振動と同じく両端が節となる振動です。
気柱の振動というのは大まかに表すと左図のような感じです
左図は定常波ができている場面というわけではありません。
あと、高校物理では長さ方向の振動しか考えません。厳密にいえば直径方向の振動もあるのですがそこまでは考えません。
。音を鳴らすと空気分子に次々に揺れが伝わっていきます。
閉じている口、閉口端で波が跳ね返されるのは不思議ではないでしょうが、開いている口、開口端においても空気分子が戻ってくるのは不思議に感じられるかもしれません。これは外部の空気分子に押し返されるためです。宇宙空間ではないので外部にも空気分子があります。しかし、閉口端と開口端では跳ね返り方が異なります。
また、空気分子は横波を伝えることができないので縦波です。縦波は横波に変換して考えます。気柱の振動は縦波を横波に変換して考えます。
閉管の固有振動
閉管において、
閉口端は空気分子が動けないので固定端となり、定常波における節となります。
もう一方の開口端は空気分子が自由に動けるので自由端となり、定常波における腹となります。
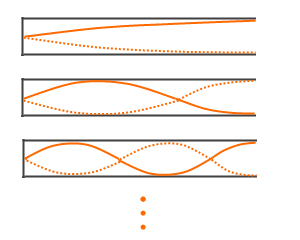片端が節、もう片端が腹という制約があるので定常波の形状パターンは左図のようになります。
超高層ビルの揺れ方もこれと同じになります。90°起こした形、1階部分が節で、最上階部分が腹、という感じです。
¼波長 
が1つの振動を基本振動、
¼波長が3つの振動を3倍振動、
¼波長が5つの振動を5倍振動、
… といいます。
閉管は奇数倍 \(2n\!-\!1\) の振動しかできません。2倍振動、4倍振動といった偶数倍の振動はありません。
\(2n\!-\!1\ (n=1,2,3,…)\) は \(m\ (m=1,3,5,…)\) と表現しても構いません。どちらも同じ意味です。奇数、ということです。
管の長さが \(l\) [m] のときの \(2n\!-\!1\)倍振動での波長を求めてみます。
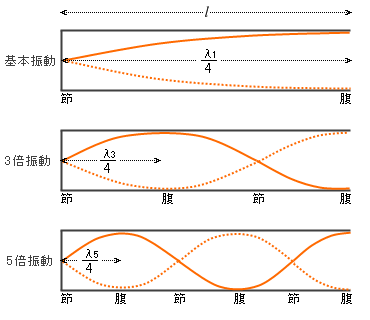
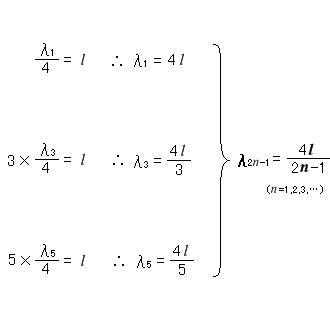
前項の＊の中で説明したのと同じイメージ図を描くと以下のようになります。
\(λ_1 = 4l\) というのは、
ということですし、
\(λ_3 = {\large\frac{4l}{3}}\) というのは、
ということですし、
\(λ_5 = {\large\frac{4l}{5}}\) というのは、
ということです。
次に振動数を求めます。音速を \(V\) [m/s] とし、振動数を \(f_{2n\!-\!1}\) [Hz] とすると、\(v = fλ\) という関係があるのでこの式に上式を代入しますと、
\(f_{2n\!-\!1} = {\large\frac{V}{\ \lambda_{2n-1}}} = {\large\frac{V}{\ \frac{4l}{\ 2n-1}}} = {\large\frac{2n-1}{\ 4l}}V\)
となります。この式をよく見ますと、\(V\) と \(l\) は定数なので、\(2n\!-\!1\) が 3、5、7、… と増えていくと \(f_{2n\!-\!1}\) も 3倍、5倍、7倍、… と増えていくことがわかります。\(2n\!-\!1\)倍振動の振動数は基本振動の振動数の \(2n\!-\!1\)倍ということです。
閉管の固有振動
\(\boldsymbol{λ_{2n-1} = {\large\frac{4l}{\ 2n-1}}}\)
\(\boldsymbol{f_{2n-1} = {\large\frac{2n-1}{\ 4l}}V}\) \((n = 1,2,3,…)\)
開管の固有振動
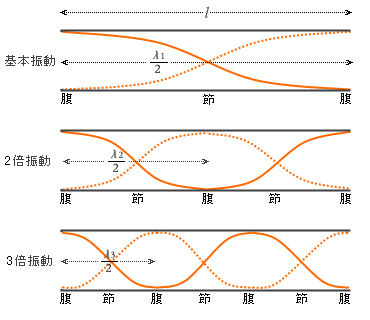
開管は両端の口が開いていて空気分子が自由に動けるので両端とも自由端となり、定常波における腹となります。
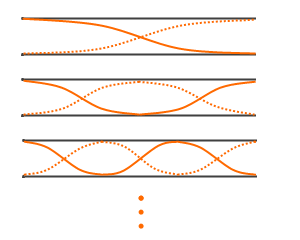定常波の形状パターンは左図のようになります。
½波長 
が1つの振動を基本振動、
½波長が2つの振動を2倍振動、
½波長が3つの振動を3倍振動、
… といいます。
管の長さが \(l\) [m] のときの \(n\)倍振動での波長を求めます。
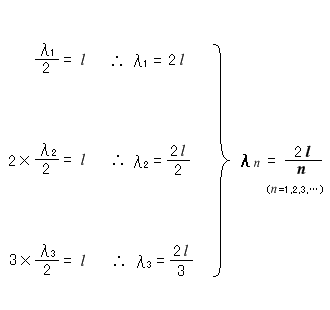
次に振動数を求めます。振動数を \(f_n\) [Hz] とし、\(v = fλ\) という関係があるのでこの式に上式を代入しますと、
\(f_n = {\large\frac{V}{\ λ_n}} = {\large\frac{V}{\ \frac{2l}{\ n\ }}} = {\large\frac{n}{\ 2l}}V\)
となります。\(V\) と \(l\) は定数なので、\(n\) が2倍になると \(f_n\) も2倍になります。\(n\)倍振動の振動数は基本振動の振動数の\(n\)倍です。
開管の固有振動
\(\boldsymbol{λ_n = {\large\frac{2l}{\ n\ }}}\)
\(\boldsymbol{f_n = {\large\frac{n}{\ 2l}}V}\) \((n = 1,2,3,…)\)
弦の振動との見比べ
・弦の固有振動 （端は節と節。\(l\) は½波長の自然数倍）
\(λ_n = {\large\frac{2l}{n}}\)
\(f_n = {\large\frac{n}{2l}\sqrt{\frac{S}{\rho}}}\) \((n=1,2,3,…)\)
・気柱（閉管）の固有振動 （端は節と腹。\(l\) は¼波長の奇数倍）
\(λ_{2n\!-\!1} = {\large\frac{4l}{2n-1}}\)
\(f_{2n\!-\!1} = {\large\frac{2n-1}{4l}}V\) \((n=1,2,3,…)\)
・気柱（開管）の固有振動 （端は腹と腹。\(l\) は½波長の自然数倍）
\(λ_n = {\large\frac{2l}{n}}\)
\(f_n = {\large\frac{n}{2l}}V\) \((n=1,2,3,…)\)
開口端補正
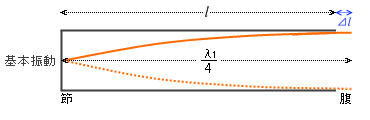
ここまでは、定常波の腹の位置が管の開口部にあるという前提で話を進めてきましたが、実験によりますと実際には定常波の腹の位置というのは管のちょっと外側にあります。
ですのでたとえば、
閉管の基本振動のときは、\({\large\frac{λ_1}{4}} = l\) のところが、
\({\large\frac{λ_1}{4}} = l + {\color{blue}Δl}\) となります。
開管のときはこれが両端ですから、\({\large\frac{λ_1}{2}} = l\) のところが、
\({\large\frac{λ_1}{2}} = l + {\color{blue}2Δl}\) となります。
これらのことを開口端補正といいます。 おおよそ、\({\color{blue}Δl} ≒ 0.6r\) （\(r\) は管の断面の半径）という関係があります。
しかし開口端補正については無視することも多いので試験等では断り書きに注意してください。