半減期
半減期とは
放射性崩壊する原子核は崩壊する確率が決まっています。確率が決まっているといっても、例えば1%の確率である場合、残りの99%の原子核も1%の確率でまた崩壊します。ですから確率といっても単位時間当たりの確率でなければ意味がありません。
いま、とある原子核が1秒当たり13%の確率で崩壊するとします。するとその個数は、1秒後に87%になり、さらに1秒後に(0.872≒)約76%、さらに1秒後約66%、さらに1秒後約57%、さらに1秒後約50%になります。つまり5秒後に約半分になります。
この半分になる時間の数値が原子核崩壊の確率を表す数値として普及していて、これを半減期といいます
半減期は単位時間当たりの崩壊確率と反比例しています。
半減期が大きければ崩壊確率は小さくなります。
。量記号としては \(T\) を用います。単位は秒であったり時間であったり年であったりします。注意が必要です。上の例では \(T\) ≒ 5 [s] です。
崩壊前の原子核の数を \(N_0\) とし、時間 \(t\) 後の原子核の数を \(N\) とすると以下のように表せます。
半減期 \(\boldsymbol{T}\)
\(\boldsymbol{N}\) = \(\boldsymbol{N_0{\large(\frac{1}{2})^\frac{t}{T}}}\)
\(N_0\) と \(T\) が定数で \(N\) と \(t\) が変数です。
\(t = T\) で半分になり、\(t = 2T\) で \({\large\frac{1}{4}}\) になります。
上の例では10秒後に \({\large\frac{1}{4}}\) になります。
指数関数をまだ習ってない人には難しいかもしれませんが、いちおうグラフを描いてみます。
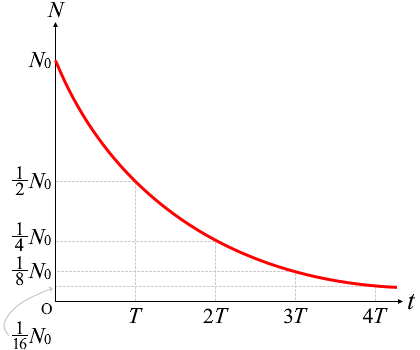
上の例において \(N_0\) を1000個とすると、5秒後に500個、10秒後に250個、15秒後に125個、20秒後に62~3個になります。
半減期の例
| 半減期 | |
|---|---|
| \(\ce{^{220}_{86}Rn}\)(ラドン220) | 55.6秒 |
| \(\ce{^{131}_{53}I}\)(ヨウ素131) | 8.0日 |
| \(\ce{^{137}_{55}Cs}\)(セシウム137) | 30.1年 |
| \(\ce{^{209}_{83}Bi}\)(ビスマス209) | 1.9×1019年 |
半減期が短い方が放射能が強い
半減期が短いということはよく崩壊するということであり、よく崩壊するということは放射線がたくさん出るということであるので、半減期が短い方が放射能が強いということになります。しかし半減期が短いのですから放射線を出している期間は短いということになります。もちろんこれらは同じ量当たりの話です。
年代測定
 植物は空気中の二酸化炭素\(\ce{CO2}\)を光合成によって取り込んで生命を維持しています。動物はそれを食べます。植物も動物も体内に炭素\(\ce{C}\)を抱えます。
植物は空気中の二酸化炭素\(\ce{CO2}\)を光合成によって取り込んで生命を維持しています。動物はそれを食べます。植物も動物も体内に炭素\(\ce{C}\)を抱えます。
炭素にはさまざまな同位体がありますが、その中で放射性があるのが \(\ce{^{14}_{6}C}\)(炭素14)です 宇宙から飛来する宇宙線が空気中の窒素に当たり生成されます。 。そして空気中において、この \(\ce{^{14}_{6}C}\) は(一般的な)\(\ce{^{12}_{6}C}\) に対してほぼ一定の割合で存在しています。
生物の体内では \(\ce{^{14}_{6}C}\) がどんどん放射性崩壊していきます。生きているうちは外部の炭素を取り込むので体内の各炭素の割合も外部と同じに保たれます。しかし死んでしまうと新たに取り込まれなくなり \(\ce{^{14}_{6}C}\) の割合がどんどん減っていきます。
\(\ce{^{14}_{6}C}\) の半減期は約5730年であり、この \(\ce{^{14}_{6}C}\) の割合を調べることによって生物がいつ死んだが測定できます。これが放射性炭素による年代測定です。